تعداد بازدید ها: 84,506
از مهمترین ابزارهای ریاضیاتی تاریخ علم، که بشر تاکنون به آن دست یافته، «انتگرال» (Integral) است. از این مفهوم میتوان بهمنظور محاسبه مساحت، حجم و طول استفاده کرد. نماد استفاده شده برای توصیف انتگرال، s کشیده است. این حرف مخفف کلمه لاتین «Sum» به معنای جمع است. برای شروع، با استفاده از مساحت سطح زیر نمودار، به معرفی این مفهوم میپردازیم. بهمنظور درک مفهوم انتگرال در ابتدا بایستی با مشتق آشنایی داشته باشید. در ادامه مفاهیمی مرتبط با انتگرال همچون انتگرال سطحی، انتگرال دوگانه و انتگرال توابع مثلثاتی را توضیح خواهیم داد.
محتوای این مطلب جهت یادگیری بهتر و سریعتر آن، در انتهای متن به صورت ویدیویی نیز ارائه شده است.
برای مشاهده ویدیوها کلیک کنید.
سوال:
مساحت سطح زیر نمودار تابع (y=f(x چقدر است؟
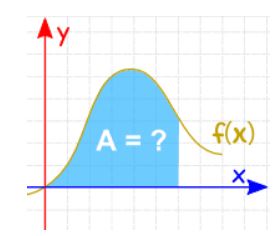
تقسیمبندی مساحت
همانطور که در شکل زیر نیز میبینید، بهمنظور محاسبه مساحت سطحِ زیر یک نمودار میتوان آن را چند قسمت کرد. برای راحتی کار عرض تمامی این بخشها، یکسان و برابر با $$\Delta x$$ در نظر گرفته میشود.
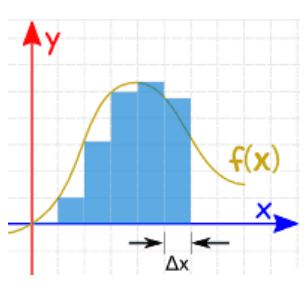
بنابراین همانگونه که در بالا بیان شد، با محاسبه مستطیلهای فرض شده، میتوان مساحت زیر نمودار را بدست آورد. احتمالا شما نیز متوجه شدهاید که مساحت محاسبه شده با مقدار مدنظر تفاوت خواهد داشت. همانطور که در شکل زیر نیز میبینید، نواحی قرمز رنگ، اختلاف مساحت مدنظر و مساحت محاسبه شده را نشان میدهند. به نظر شما چطور میتوان مقدار بدست آمده را به مقدار واقعی نزدیکتر کرد؟
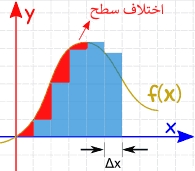
حال با همان روش قبلی، سطوح را تقسیمبندی کنید، اما این بار فواصل $$\Delta x$$ را کوچکتر در نظر بگیرید. در شکل زیر نیز مشخص است که با کوچک کردن این فواصل، مساحت محاسبه شده و مساحت مدنظر به یکدیگر نزدیکتر شدهاند.
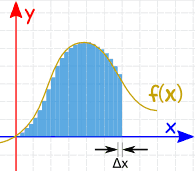
بر همین مبنا، مطابق شکل زیر اگر $$\Delta x$$ به صفر میل کند، (مساحت به بینهایت بخش تقسیم شود) مساحت مد نظر ما نیز بدست میآید.
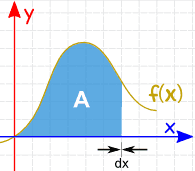
محاسبه مساحت
به نظر میرسد با محاسبه مساحت بینهایت مستطیل، میتوان سطح زیر یک نمودار را بدست آورد. اما سوال اینجا است که به راستی چگونه میتوان بینهایت عدد را محاسبه کرد؟ واقعیت این است که نیازی نیست تمامی این مساحتها را بدانیم، چراکه نیوتن راه کوتاهتری را به ما نشان داده. او اثبات کرده که انتگرال و مشتق عکس هم هستند. برای درک بهتر به مثالهای زیر توجه فرمایید.
توجه داشته باشید که به منظور حل یک انتگرال میتوان از تکنیکهای مختلفی استفاده کرد. معروفترینِ این روشها، جزء به جزء، تغییر متغیر، روشهای عددی و تجزیه کسر (کسرهای جزئی) هستند؛ البته در این لینک به کلیات روشهای حل نیز اشاره شده است.
مثال ۱
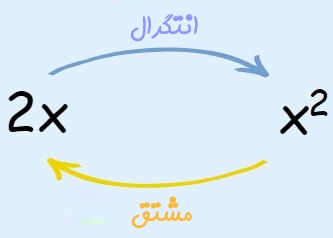
انتگرال تابع y=2x را بیابید.
میدانیم که مشتق تابع $$x^2$$ برابر با ۲x است. بنابراین انتگرال 2x برابر با x2 میشود.
در بخش دوم در مورد قوانین حاکم در حل انتگرال یک تابع، بیشتر بحث خواهیم کرد. توجه داشته باشید که مساحت را میتوان با استفاده از انتگرال دوگانه نیز بدست آورد.
نماد انتگرال
همانطور که در بالا نیز بیان شد، نماد استفاده شده به منظور توصیف انتگرال، حرف s کشیده است. پس از این نماد، تابعی قرار میگیرد که هدف ما محاسبه انتگرال آن است. سپس dx قرار میگیرد که نشان دهنده عرض هرکدام از مستطیلها است.

در حالت کلی قالب نوشتن یک معادله انتگرالی به شکل زیر است.
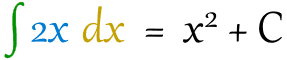
نماد انتگرالی شکل استفاده شده در ویولن با هدف تقویت فرکانسهای صوتی است و ربطی به ریاضیات ندارد!

C به چه معنا است؟
در مثال شماره ۱، پاسخ را برابر با $$x^2$$ بدست آوردیم، اما چرا در جواب نهایی، آن را با C جمع کردیم؟ عدد C ثابت انتگرال است. دلیل قرار گرفتن C این است که اگر تابع $$x^2$$ را با هر عدد ثابتی جمع کنیم و سپس از آن مشتق بگیریم، همچنان 2x ظاهر میشود. در حقیقت مشتق توابع $$ x^2+9 ,x^2+1025,x^2+4 $$ همگی برابر با ۲x هستند، در نتیجه تمامی آنها را میتوان به عنوان پاسخ انتگرال مثال ۱ در نظر گرفت.
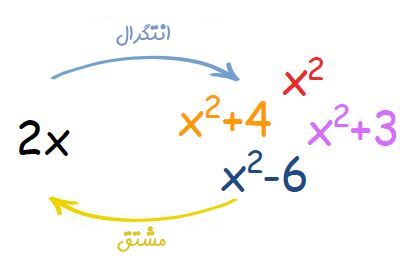
از این رو بهمنظور بیان این اعداد از ثابت C استفاده میکنیم.
مخزن آب
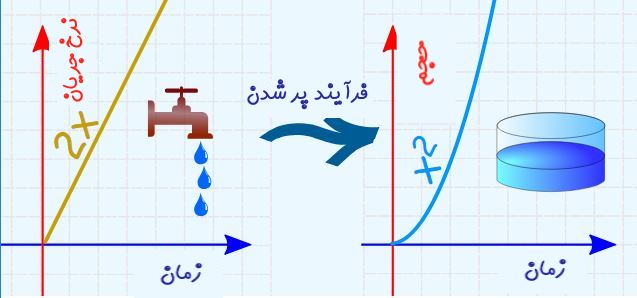
انتگرالگیری را میتوان مشابه با مخزن آبی دانست که توسط یک شیر در حال پر شدن است. تابع ورودی، همان نرخ جریان آب در هر لحظه است. با انتگرالگیری از این نرخ (جمع زدن مقادیر آب اضافه شده در هر لحظه)، میتوان حجم آب موجود درون مخزن را یافت.
اگر نرخ جریان ورودی مطابق با تابع 2t تغییر کند، حجم کلی آب موجود در مخزن، در زمان t برابر با $$t^2$$ است. [ با فرض اینکه در حالت اولیه مخزن خالی بوده باشد.]
مثال ۲
مخزنی را در نظر بگیرید که جریان آب با نرخ $$2t \space {liter \over s}$$ به آن ریخته میشود. با فرض اینکه مخزن در حالت اولیه خالی بوده باشد، حجم آب موجود در مخزن پس از گذشت زمان ۳ و ۴ ثانیه چقدر است؟
پس از گذشت زمان ۳ ثانیه، نرخ جریان ورودی به مخزن برابر است با:
$$\large 2t = 2×3 = 6 \enspace {liter \over s}$$
همچنین برای محاسبه حجم آب ریخته شده به مخزن، میتوان از تابع 2t، به شکل زیر انتگرال گرفت.
$$\large = \int 2t dt=t^2 = 3^2 = 9 $$
در نتیجه حجم آب موجود در مخزن، در لحظه ۳ ثانیه برابر با ۹ لیتر است. به همین شکل در لحظه t=4 نیز حجم آب وارد شده به مخزن، برابر با لیتر $$۴^2=16$$ خواهد بود.
همین فرآیند را میتوان برعکس نیز انجام داد. یعنی با داشتن مقدار آب درون مخزن، در هر لحظه، نرخ جریان ورودی به آن را در همان لحظه بدست آورد. برای مثال فرض کنید در یک لحظه مشخص میزان آب درون مخزن برابر با ۱۶ لیتر باشد. از آنجایی که حجم آب درون مخزن با استفاده از رابطه $$V=t^2$$ محاسبه میشود، میتوان گفت:
$$\large V=t^2=16 \rightarrow t= \sqrt {16} = 4 \enspace s$$
$$\large \rightarrow \enspace \enspace 2t=2×4=8 \enspace {lit \over s}$$
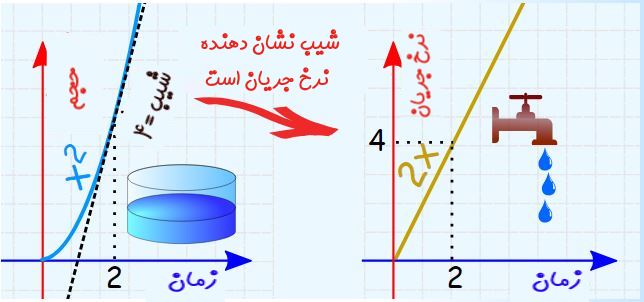
در حقیقت دو بیان زیر معادل هم هستند.
انتگرال نرخ جریان ورودی، حجم آب موجود در مخزن را محاسبه میکند ≡ شیب حجم آب موجود در مخزن، نرخ جریان ورودی به آن را نشان میدهد.
انتگرال دیگر توابع
در بالا به اندازه کافی در مورد تابع 2x صحبت کردیم. در این قسمت قصد داریم تا در مورد نحوه انتگرالگیریِ دیگر توابع بحث کنیم.
مثال ۳
انتگرال تابع $$f(x)=cos(x)$$ را بیابید.
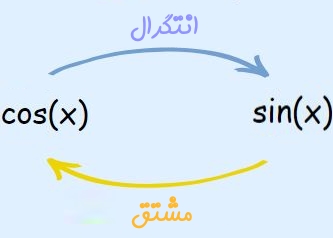
همانطور که میدانید برای محاسبه انتگرال این تابع، بایستی به دنبال رابطهای بگردیم که مشتق آن برابر با (cos (x شود. احتمالا میدانید که تابع مدنظر (sin (x است، چراکه مشتق آن برابر با (cos (x میشود. بنابراین میتوان گفت:
$$\large \int cos (x) dx= sin(x)+C$$
مثال ۴
به نظر شما انتگرال تابعی که به شکل $$f(x)=x^n$$ باشد، به چه صورت است.
برای محاسبه چنین انتگرالی بایستی فکر کنید که مشتق چه تابعی برابر با $$f(x)=x^n$$ میشود. تابعی به شکل زیر را در نظر بگیرید:
$$\large {{x^{n+1} \over {n+1}} +C}$$
مشتق این تابع برابر با $$f'(x)=x^n$$ است. بنابراین میتوان گفت:
$$\large \int \enspace x^n dx = {x^{n+1} \over {n+1}}$$
مثال ۵
حاصل $$ \int x^3 dx $$ را بیابید.
با جایگذاری ۳ بهجای n در معادله بالا داریم:
$$\large \rightarrow \int x^3 dx={x^4 \over 4} + C $$
انتگرال معین و نامعین
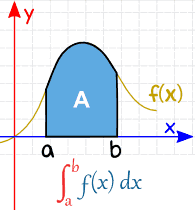
تاکنون انتگرالهایی که محاسبه شد، همگی نامعین بودند. انتگرال معین اصطلاحی است که به منظور محاسبه انتگرال در بازهای مشخص استفاده میشود. در حقیقت انتگرال معین، مساحت زیر منحنی در بازه مفروض را (مثلا a تا b) محاسبه میکند. شکل زیر مفهوم انتگرال معین را نشان داده است.
در بخش آینده، روشهایی را ارائه خواهیم داد (مانند روش تجزیه کسر) که با استفاده از آنها قادر خواهید بود تا انتگرال توابع مختلف را محاسبه کنید. در آینده انتگرال دوگانه و نحوه محاسبه طول قوس منحنی به کمک انتگرال را نیز توضیح خواهیم داد. همچنین در صورت علاقهمندی میتوانید نحوه بدست آوردن انتگرال توابع مثلثاتی را نیز مطالعه فرمایید.
اگر مطلب بالا برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشی دروس دبیرستان
- مجموعه آموزشهای ریاضی و فیزیک
- آموزش ریاضیات عمومی ۱
- انتگرال به زبان ساده — بخش دوم: روشهای محاسبه
- انتگرال گیری جزء به جزء — به زبان ساده
- انتگرال توابع مثلثاتی — به زبان ساده
- انتگرال دوگانه — به زبان ساده
- محاسبه انتگرال به روش تغییر متغیر — از صفر تا صد
^^
مفهوم و نماد انتگرال
انتگرال توابع ساده
مجید عوض زاده
«مجید عوضزاده»، فارغ التحصیل مقطع کارشناسی ارشد رشته مهندسی مکانیک از دانشگاه تهران است. فیزیک، ریاضیات و مهندسی مکانیک از جمله مباحث مورد علاقه او هستند که در رابطه با آنها تولید محتوا میکند.
بر اساس رای 14 نفر
آیا این مطلب برای شما مفید بود؟
