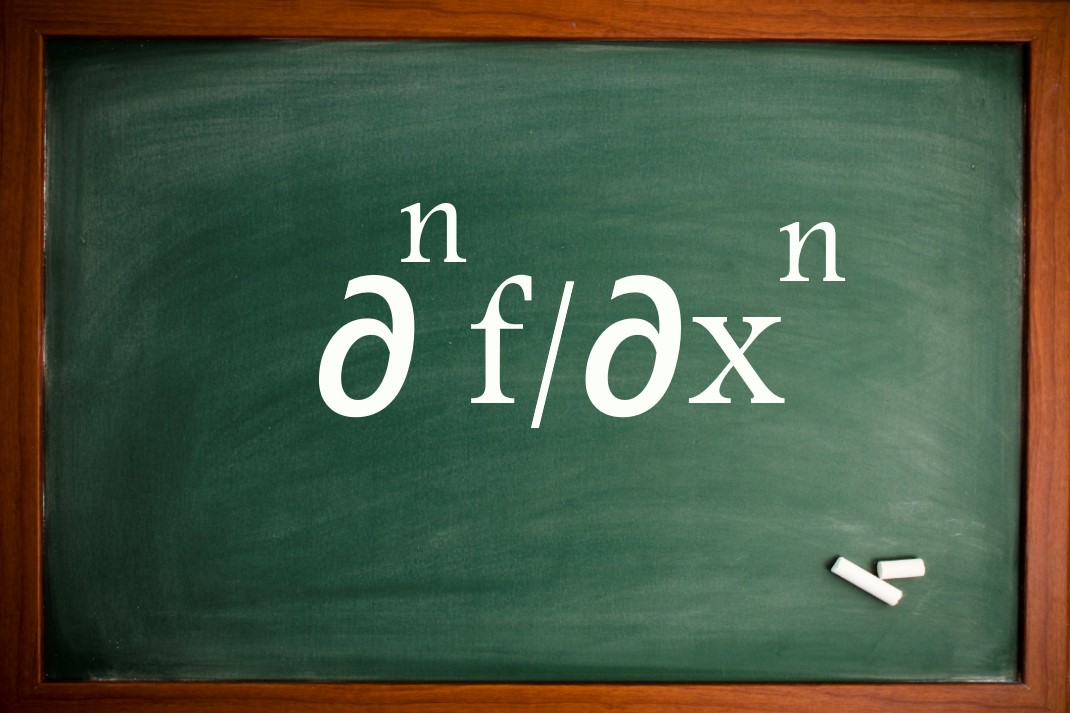تعداد بازدید ها: 13,841
پیشتر در بلاگ فرادرس مفاهیم مشتق جزئی بیان شدند. در این مطلب قصد داریم تا مشتق جزئی مراتب بالاتر را توضیح دهیم.
فیلم آموزش مشتق جزئی مراتب بالاتر — به زبان ساده (+ دانلود فیلم آموزش رایگان)
فرمول مشتق مراتب بالاتر
تابعی چند متغیره همچون (f(x,y را در نظر بگیرید. این تابع نسبت به دو متغیر x و y تغییر میکند. از این رو میتوان تغییرات تابع را نسبت به هریک از این متغیرها محاسبه کرد. توجه داشته باشید که تابع دو متغیره بوده و ۴ حالت میتواند برای مشتق مرتبه دوم وجود داشته باشد. در ادامه روابط مربوط به این ۴ حالت نشان داده شده است.
$$ \large \begin {align*} { \left ( { { f _ x } } \right ) _ x } & = { f _ { x \, x } } = \frac { \partial } { { \partial x } } \left ( { \frac { { \partial f } } { { \partial x } } } \right ) = \frac { { { \partial ^ 2 } f } } { { \partial { x ^ 2 } } } \\ { \left ( { { f _ x } } \right ) _ y } & = { f _ { x \, y } } = \frac { \partial } { { \partial y } } \left ( { \frac { { \partial f } } { { \partial x } } } \right ) = \frac { { { \partial ^ 2 } f } } { { \partial y \partial x } } \\ { \left ( { { f _ y } } \right ) _ x } & = { f _ { y \, x } } = \frac { \partial } { { \partial x } } \left ( { \frac { { \partial f } } { { \partial y } } } \right ) = \frac { { { \partial ^ 2 } f } } { { \partial x \partial y } } \\ { \left ( { { f _ y } } \right ) _ y } & = { f _ { y \, y } } = \frac { \partial } { { \partial y } } \left ( { \frac { { \partial f } } { { \partial y } } } \right ) = \frac { { { \partial ^ 2 } f } } { { \partial { y ^ 2 } } } \end {align*} $$
تمامی این مشتقات از مرتبه ۲ هستند. شاید نکته جالب در روابط فوق تفاوتِ فرمولِ دو مشتق $$ { f _ { x \, y } } = \frac { \partial } { { \partial y } } \left ( { \frac { { \partial f } } { { \partial x } } } \right ) $$ و $$ { f _ { y \, x } } = \frac { \partial } { { \partial x } } \left ( { \frac { { \partial f } } { { \partial y } } } \right ) $$ است. همانطور که احتمالا شما نیز متوجه شدهاید، مشتق در ابتدا نسبت به اندیس چپ و سپس نسبت به اندیس سمت راست گرفته میشود. در ادامه مثالهایی ارائه شده، که مطالعه آنها را توصیه میکنیم.
مثال ۱
تمامی مشتقات مرتبه دوم تابع $$ f \left ( { x , y } \right ) = \cos \left ( { 2 x } \right ) – { x ^ 2 } { { \bf { e } } ^ { 5 y } } + 3 { y ^ 2 } $$ را بیابید.
در ابتدا بایستی مشتقات نسبت به x و y به طور جداگانه محاسبه شود. بنابراین داریم:
$$ \large \begin {align*} { f _ x } \left ( { x , y } \right ) & = – 2 \sin \left ( { 2 x } \right ) – 2 x { { \bf { e } } ^ { 5 y } } \\ { f _ y } \left ( { x , y } \right ) & = – 5 { x ^ 2 } { { \bf { e } } ^ { 5 y } } + 6 y \end {align*} $$
حال از دو عبارت بدست آمده در بالا، نسبت به x و y مشتق میگیریم.
$$ \large \begin {align*} { f _ { x x } } & = – 4 \cos \left ( { 2 x } \right ) – 2 { { \bf { e } } ^ { 5 y } } \\ { f _ { x y } } & = – 1 0 x { { \bf { e } } ^ { 5 y } } \\ { f _ { y x } } & = – 1 0 x { { \bf{ e } } ^ { 5 y } } \\ { f _ { y y } } & = – 2 5 { x ^ 2 } { { \bf{ e } } ^ { 5 y } } + 6 \end {align*} $$
همانطور که میبینید در روابط بالا از $$ \left( {x,y} \right) $$ استفاده نشده است. البته میتوان از این نماد استفاده کرد، اما در شکل استاندارد معمولا این نماد به کار گرفته نمیشود. شاید این سوال برایتان مطرح شده باشد، که در چه زمانی میتوان مشتقات fxy و fyx را برابر در نظر گرفت؛ از این رو در ادامه قضیهای مطرح شده که این موضوع در آن مطرح شده است.
قضیه: فرض کنید تابع f در ناحیه D تعریف شده باشد. اگر مشتقات $$ { f _ { x y } } $$ و $$ { f _ { y x } } $$ در نقطه مذکور پیوسته باشند، در این صورت رابطه زیر برقرار خواهد بود.
$$ \large { f _ { x y } } \left ( { a , b } \right ) = { f _ { y x } } \left ( { a , b } \right ) $$
مثال ۲
قضیه بیان شده در بالا را برای تابع $$ f \left ( { x , y } \right ) = x { { \bf { e } } ^ { – { x ^ 2 } { y ^ 2 } } } $$ نشان دهید.
در ابتدا مشتق مرتبه اول تابع را به صورت زیر بدست میآوریم.
$$ \large \begin {align*} { f _ x } \left ( { x , y } \right ) & = { { \bf {e} } ^ { – { x ^ 2 } { y ^ 2 } } } – 2 { x ^ 2 } { y ^ 2 } { { \bf { e } } ^ { – { x ^ 2 } { y ^ 2 } } } \\ { f _ y } \left ( { x , y } \right ) & = – 2 y { x ^ 3 }{ { \bf { e } } ^ { – { x ^ 2 } { y ^ 2 } } } \end {align*} $$
حال میتوان مشتقات $$ { f _ { x y } } $$ و $$ { f _ { y x } } $$ را مطابق با روابط زیر بدست آورد.
$$ \large \begin {align*} { f _ { x y } } \left ( { x , y } \right ) & = – 2 y { x ^ 2 } { { \bf { e } } ^ { – { x ^ 2 } { y ^ 2 } } } – 4 { x ^ 2 } y { { \bf { e } } ^ { – { x ^ 2 } { y ^ 2 } } } + 4 { x ^ 4 } { y ^ 3 } { { \bf { e } } ^ { – { x ^ 2 } { y ^ 2 } } } = – 6 { x ^ 2 } y { { \bf{ e } } ^ { – { x ^ 2 } { y ^ 2 } } } + 4 { x ^ 4 } { y ^ 3 }{ { \bf { e } } ^ { – { x ^ 2 } { y ^ 2 } } } \\ { f _ { y x } } \left ( { x , y } \right ) & = – 6 y { x ^ 2 } { { \bf { e } } ^ { – { x ^ 2 } { y ^ 2 } } } + 4 { y ^ 3 } { x ^ 4 } { { \bf{e} } ^ { – { x ^ 2 } { y ^ 2 } } } \end {align*} $$
تاکنون تنها مشتقات مرتبه دوم را مورد بررسی قرار دادیم. توجه داشته باشید که میتوان مشتقات جزئی را نیز تا مراتب بالاتر محاسبه کرد. در ادامه دو نمونه از مشتقات مرتبه سوم نشان داده شده است.
$$ \large \begin {align*} { f _ { x \, y \, x } } & = { \left ( { { f _ { x y } } } \right ) _ x } = \frac { \partial } { { \partial x } } \left ( { \frac { { { \partial ^ 2 } f } } { { \partial y \partial x } } } \right ) = \frac { { { \partial ^ 3 } f } } { { \partial x \partial y \partial x } } \\ { f _ { y \, x\, x } } & = { \left ( { { f _ { y x } } } \right ) _ x } = \frac { \partial } { { \partial x } } \left ( { \frac { { { \partial ^ 2 } f } } { { \partial x \partial y } } } \right ) = \frac { { { \partial ^ 3 } f } } { { \partial { x ^ 2 } \partial y } } \end {align*} $$
توجه داشته باشید که قضیه بیان شده در بالا برای نقاطی که در آنها مشتق پیوسته است، در مراتب بالاتر نیز برقرار خواهد بود. برای نمونه در این نقاط، سه مشتق جزئی زیر با هم برابر هستند.
$$ \large { f _ { x \, x \, y } } = { f _ { x \, y \, x } } = { f _ { y \, x \, x } } $$
در حالت کلی قضیه فوق برای هر تابعی با هر تعداد متغیری برقرار خواهد بود. تنها نکته مهم برابر بودن تعداد هر متغیر در دو سمت رابطه است. برای نمونه دو مشتق زیر با هم برابر هستند و دلیل آن برابر بودن تعداد s,r,t در دو طرف رابطه است.
$$ \large { f _ { s \, s \, r\, t\, s\, r\, r } } = { f _ { t \, r \, s \, r \, s \, s \, r } } $$
مثال ۳
مشتقات زیر را بیابید.
- $$ \large { f _ { x \, x \, y \, z \, z } } $$ برای تابع $$ \large f \left ( { x , y , z } \right ) = { z ^ 3 } { y ^ 2 } \ln \left ( x \right ) $$
- $$ \large \displaystyle \frac { { { \partial ^ 3 } f } } { { \partial y \partial { x ^ 2 } } } $$ برای تابع $$ \large f \left ( { x , y } \right ) = { { \bf{ e } } ^ { x y } } $$
a: توجه داشته باشید که مشتقگیری از چپ به راست انجام میشود. بنابراین داریم:
$$ \large { f _ x } = \frac { { { z ^ 3 } { y ^ 2 } } } { x } $$
$$ \large { f _ { x x } } = – \frac { { { z ^ 3 } { y ^ 2 } } } { { { x ^ 2 } } } $$
$$ \large { f _ { x x y } } = – \frac { { 2 { z ^ 3 } y } } { { { x ^ 2 } } } $$
$$ \large { f _ { x x y z } } = – \frac { { 6 { z ^ 2 } y } } { { { x ^ 2 } } } $$
$$ \large { f _ { x x y z z } } = – \frac { { 1 2 z y } } { { { x ^ 2 } } } $$
b: در این حالت نیز در ابتدا دو بار نسبت به x و در مرحله بعد نسبت y مشتقگیری میکنیم.
$$ \large \frac { { \partial f } } { { \partial x } } = y { { \bf { e } } ^ { x y } } $$
$$ \large \frac { { { \partial ^ 2 } f } } { { \partial { x ^ 2 } } } = { y ^ 2 } { { \bf{ e } } ^ { x y } } $$
$$ \large \frac { { { \partial ^ 3 } f } } { { \partial y \partial { x ^ 2 } } } = 2 y { { \bf{ e } } ^ { x y } } + x { y ^ 2 } { { \bf{ e } } ^ { x y } } $$
در صورت علاقهمندی به مباحث مرتبط در زمینه ریاضی، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای ریاضیات
- مجموعه آموزشهای ریاضی و فیزیک
- آموزش ریاضی عمومی ۲
- تابع چند متغیره — به زبان ساده
- تابع برداری — از صفر تا صد
^^
«مجید عوضزاده»، فارغ التحصیل مقطع کارشناسی ارشد رشته مهندسی مکانیک از دانشگاه تهران است. فیزیک، ریاضیات و مهندسی مکانیک از جمله مباحث مورد علاقه او هستند که در رابطه با آنها تولید محتوا میکند.
بر اساس رای 20 نفر
آیا این مطلب برای شما مفید بود؟