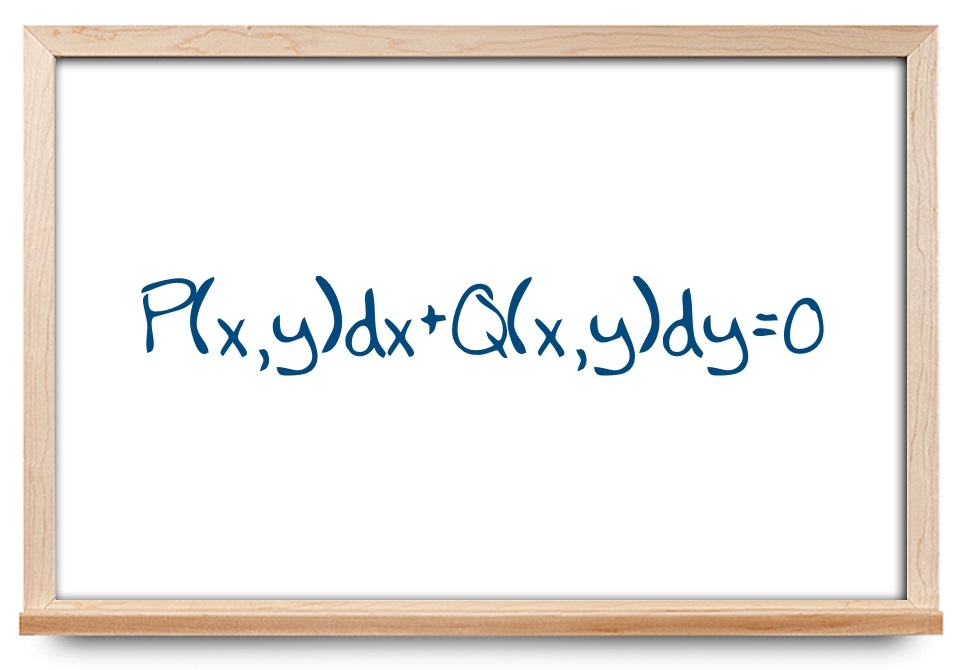معادله دیفرانسیل کامل

تعداد بازدید ها: 17,055

در آموزش‌های قبلی مجله فرادرس، با معادلات دیفرانسیل آشنا شدیم. در این آموزش‌ها، روش‌های حل معادلات دیفرانسیل مرتبه اول، معادلات دیفرانسیل مرتبه دوم و معادلات مرتبه بالاتر را معرفی کردیم. همچنین به روش حل معادلات خاص، مانند معادله دیفرانسیل چبیشف پرداختیم. در این آموزش، دسته دیگری از معادلات دیفرانسیل را به‌نام «معادلات دیفرانسیل کامل» (Exact Differential Equations) معرفی، و روش حل آن‌ها را بیان خواهیم کرد.

فیلم آموزش معادلات دیفرانسیل کامل — به زبان ساده (+ دانلود فیلم آموزش گام به گام)

تعریف

معادله دیفرانسل به‌فرمِ

$${P\left( {x,y} \right)dx + Q\left( {x,y} \right)dy }={ 0}$$

را یک معادله دیفرانسیل کامل می‌نامیم، اگر تابع دومتغیره $$u\left( {x,y} \right)$$ با مشتقات جزئی پیوسته وجود داشته باشد، به‌طوری که:

$${du\left( {x,y} \right) \text{ = }}\kern0pt{ P\left( {x,y} \right)dx + Q\left( {x,y} \right)dy.}$$

جواب عمومی یک معادله دیفرانسیل کامل، به‌صورت زیر است:

$$u\left( {x,y} \right) = C$$

که در آن، $$C$$ یک ثابت دلخواه است.

آزمون کامل بودن

فرض کنید توابع $$P\left( {x,y} \right)$$ و $$Q\left( {x,y} \right)$$ در دامنه مشخص $$D$$، مشتقات جزئی پیوسته داشته باشند. معادله دیفرانسیل $$P\left( {x,y} \right)dx +Q\left( {x,y} \right)dy= 0$$، یک معادله کامل است اگر و تنها اگر تساوی زیر برقرار باشد:

$$\frac{{\partial Q}}{{\partial x}} = \frac{{\partial P}}{{\partial y}}.$$

الگوریتم حل معادلات دیفرانسیل کامل

۱. ابتدا باید با استفاده از آزمون، از کامل بودن معادله دیفرانسیل مطمئن شویم:

 $$\frac{{\partial Q}}{{\partial x}} = \frac{{\partial P}}{{\partial y}}.$$

2. دستگاه معادلات دیفرانسیل زیر را تشکیل می‌دهیم که تابع $$u\left( {x,y} \right)$$ را تعریف می‌کند:

$$\left\{ \begin{array}{l}
\frac{{\partial u}}{{\partial x}} = P\left( {x,y} \right)\\
\frac{{\partial u}}{{\partial y}} = Q\left( {x,y} \right)
\end{array} \right..$$

۳. از معادله اول نسبت به $$x$$ انتگرال گرفته و به‌جای ثابت $$C$$ انتگرال، یک تابع مجهول از $$y$$ قرار می‌دهیم:

$${u\left( {x,y} \right) \text{ = }}\kern0pt{ \int {P\left( {x,y} \right)dx} + \varphi \left( y \right).}$$

۴. از رابطه اخیر، نسبت به $$y$$ مشتق می‌گیریم و تابع $$u\left( {x,y} \right)$$ را در معادله دوم جایگذاری می‌کنیم:

$${\frac{{\partial u}}{{\partial y}} \text{ = }}\kern0pt
{\frac{\partial }{{\partial y}}\left[ {\int {P\left( {x,y} \right)dx} + \varphi \left( y \right)} \right] }
= {Q\left( {x,y} \right).}$$

با کمی عملیات جبری روی معادله اخیر، می‌توان توصیف تابع مجهول $${\varphi \left( y \right)}$$ را نوشت:

$${\varphi’\left( y \right) }
= {Q\left( {x,y} \right) }-{ \frac{\partial }{{\partial y}}\left( {\int {P\left( {x,y} \right)dx} } \right).}$$

۵. با انتگرال‌گیری از تساوی اخیر، تابع $${\varphi \left( y \right)}$$، و در نتیجه تابع $$u\left( {x,y} \right)$$ به‌دست می‌آید:

$${u\left( {x,y} \right) \text{ = }}\kern0pt{ \int {P\left( {x,y} \right)dx} + \varphi \left( y \right).}$$

6. در نهایت، جواب عمومی معادله دیفرانسیل کامل به‌صورت زیر خواهد بود:

$$u\left( {x,y} \right) = C.$$

نکته: در گام ۳، می‌توان به‌جای انتگرال گرفتن معادله اول نسبت به $$x$$، از معادله دوم نسبت به $$y$$ انتگرال گرفت. بنابراین، بعد از انتگرال‌گیری باید تابع مجهول $${\psi \left( x \right)}$$ را پیدا کنیم.

مثال‌ها

در ادامه، چند مثال حل‌شده را برای درک بهتر حل معادلات دیفرانسیل کامل بیان می‌کنیم.

مثال ۱

معادله دیفرانسیل زیر را حل کنید.

$$2xydx +\left( {{x^2} + 3{y^2}} \right)dy= 0$$

حل: معادله بالا، یک معادله کامل است، زیرا مشتقات جزئی آن یکسان هستند:

$${{\frac{{\partial Q}}{{\partial x}} }={ \frac{\partial }{{\partial x}}\left( {{x^2} + 3{y^2}} \right) }={ 2x,\;\;}}\kern-0.3pt
{{\frac{{\partial P}}{{\partial y}} }={ \frac{\partial }{{\partial y}}\left( {2xy} \right) }={ 2x.}}$$

دستگاه معادلات دیفرانسیل زیر را برای یافتن $$u\left( {x,y} \right)$$ تشکیل می‌دهیم:

$$\left\{ \begin{array}{l}
\frac{{\partial u}}{{\partial x}} = 2xy\\
\frac{{\partial u}}{{\partial y}} = {x^2} + 3{y^2}
\end{array} \right..$$

با انتگرال‌گیری از معادله اول نسبت به $$x$$، داریم:

$${u\left( {x,y} \right) = \int {2xydx} }={ {x^2}y + \varphi \left( y \right).}$$

جایگذاری عبارت $$u\left( {x,y} \right)$$ در معادله دوم دستگاه، به عبارت زیر منجر خوهد شد:

$${{\frac{{\partial u}}{{\partial y}} }={ \frac{\partial }{{\partial y}}\left[ {{x^2}y + \varphi \left( y \right)} \right] }={ {x^2} + 3{y^2},\;\;}}\\
\Rightarrow
{{{x^2} + \varphi’\left( y \right) }={ {x^2} + 3{y^2},\;\;}}\Rightarrow
{\varphi’\left( y \right) = 3{y^2}.}$$

اگر از معادله اخیر انتگرال بگیریم، تابع مجهول $${\varphi \left( y \right)}$$ به‌دست می‌آید:

$$\varphi \left( y \right) = \int {3{y^2}dy} = {y^3}$$

بنابراین، جواب عمومی معادله دیفرانسسل کامل، به‌صورت زیر خواهد بود:

$${x^2}y + {y^3} = C$$

که در آن، $$C$$ یک ثابت اختیاری است.

مثال ۲

جواب معادله دیفرانسیل زیر را به‌دست آورید:

$$\left( {6{x^2} – y + 3} \right)dx +\left( {3{y^2} – x – 2} \right)dy=0$$

حل: ابتدا کامل بودن معادله را بررسی می‌کنیم:

$${{\frac{{\partial Q}}{{\partial x}} }={ \frac{\partial }{{\partial x}}\left( {3{y^2} – x – 2} \right) }={ – 1,\;\;}}\kern-0.3pt
{{\frac{{\partial P}}{{\partial y}} }={ \frac{\partial }{{\partial y}}\left( {6{x^2} – y + 3} \right) }={ – 1.}}$$

بنابراین، معادله دیفرانسیل، کامل است. در ادامه، دستگاه معادلات را برای تعیین تابع $$u\left( {x,y} \right)$$ تشکیل می‌دهیم:

$$\left\{ \begin{array}{l}
\frac{{\partial u}}{{\partial x}} = P\left( {x,y} \right) = 6{x^2} – y + 3\\
\frac{{\partial u}}{{\partial y}} = Q\left( {x,y} \right) = 3{y^2} – x – 2
\end{array} \right.$$

در ادامه، با فرض ثابت بودن $$y$$، از معادله اول نسبت به متغیر $$x$$ انتگرال می‌گیریم. در نتیجه، داریم:

$${u\left( {x,y} \right) }={ \int {\left( {6{x^2} – y + 3} \right)dx} } \\
= {\frac{{6{x^3}}}{3} – xy + 3x + \varphi \left( y \right) }
= {2{x^3} – xy + 3x + \varphi \left( y \right).}$$

در رابطه بالا، تابع مشتق‌پذیر پیوسته $$\varphi \left( y \right)$$ را به‌جای ثابت $$C$$ در نظر گرفته‌ایم.

با قرار دادن $$u\left( {x,y} \right)$$ در معادله دوم دستگاه، داریم:

$$\require{cancel}
{\frac{{\partial u}}{{\partial y}} \text{ = }}\kern0pt
{\frac{\partial }{{\partial y}}\left[ {2{x^3} – xy + 3x + \varphi \left( y \right)} \right] }
= { – \cancel{x} + \varphi’\left( y \right) }
= {3{y^2} – \cancel{x} – 2.}$$

در نتیجه، معادله مشتق $$\varphi’\left( y \right)$$‌ به‌صورت زیر است:

$$\varphi’\left( y \right) = 3{y^2} – 2.$$

با انتگرال‌گیری از معادله بالا، تابع $$\varphi \left( y \right)$$ به‌دست می‌آید:

$${\varphi \left( y \right) }={ \int {\left( {3{y^2} – 2} \right)dy} }={ {y^3} – 2y.}$$

بنابراین، تابع $$u\left( {x,y} \right)$$ برابر است با:

$${u\left( {x,y} \right) }={ 2{x^3} – xy + 3x }+{ {y^3} }-{ 2y.}$$

در نهایت، جواب عمومی معادله با عبارت ضمنی زیر توصیف می‌شود:

$${2{x^3} – xy + 3x + {y^3} }-{ 2y }={ C}$$

که در آن، $$C$$ یک عدد حقیقی اختیاری است.

مثال ۳

معادله دیفرانسیل زیر را حل کنید:

$${e^y}dx +\left( {2y + x{e^y}} \right)dy=0$$

حل: ابتدا کامل بودن معادله را بررسی می‌کنیم:

$${{\frac{{\partial Q}}{{\partial x}} }={ \frac{\partial }{{\partial x}}\left( {2y + x{e^y}} \right) }={ {e^y},\;\;}}\kern-0.3pt
{{\frac{{\partial P}}{{\partial y}} }={ \frac{\partial }{{\partial y}}\left( {{e^y}} \right) }={ {e^y}.}}$$

می‌بینیم که تساوی $${\frac{{\partial Q}}{{\partial x}}\normalsize} = {\frac{{\partial P}}{{\partial y}}\normalsize}$$ برقرار است، بنابراین، معادله کامل است. اکنون تابع $$u\left( {x,y} \right)$$ را از دستگاه معادلات دیفرانسیل زیر پیدا می‌کنیم:

$$\left\{ \begin{array}{l}
\frac{{\partial u}}{{\partial x}} = {e^y}\\
\frac{{\partial u}}{{\partial y}} = 2y + x{e^y}
\end{array} \right..$$

در نتیجه، داریم:

$${u\left( {x,y} \right) = \int {P\left( {x,y} \right)dx} }
= {\int {{e^y}dx} }={ x{e^y} + \varphi \left( y \right).}$$

اکنون، با مشتق‌گیری از $$u$$ نسبت به $$y$$ می‌توانیم مشتق $$\varphi’\left( y \right)$$ را حساب کنیم:

$${{\frac{{\partial u}}{{\partial y}} }={ \frac{\partial }{{\partial y}}\left[ {x{e^y} + \varphi \left( y \right)} \right] }={ 2y + x{e^y},\;\;}}\\
\Rightarrow
{{\cancel{x{e^y}} + \varphi’\left( y \right) }={ 2y + \cancel{x{e^y}},\;\;}}\\ \Rightarrow
{\varphi’\left( y \right) = 2y.}$$

در نتیجه، تابع $${\varphi \left( y \right)}$$‌ به‌دست می‌آید:

$${\varphi \left( y \right) = \int {2ydy} = {y^2},\;\;}\Rightarrow
{u\left( {x,y} \right) = x{e^y} + \varphi \left( y \right) }
= {x{e^y} + {y^2}.}$$

در نهایت، پاسخ معادله دیفرانسیل به‌صورت زیر است:

$$x{e^y} + {y^2} = C.$$

مثال ۴

معادله دیفرانسیل زیر را حل کنید:

$$\left( {2xy – \sin x} \right)dx +\left( {{x^2} – \cos y} \right)dy=0$$

حل: معادله فوق کامل است، زیرا:

$${\frac{{\partial Q}}{{\partial x}} }={ \frac{\partial }{{\partial x}}\left( {{x^2} – \cos y} \right) }={ 2x }
= {\frac{{\partial P}}{{\partial y}} }={ \frac{\partial }{{\partial y}}\left( {2xy – \sin x} \right) }={ 2x.}$$

تابع $$u\left( {x,y} \right)$$ را از دستگاه معادلات زیر پیدا می‌کنیم:

$$\left\{ \begin{array}{l}
\frac{{\partial u}}{{\partial x}} = 2xy – \sin x\\
\frac{{\partial u}}{{\partial y}} = {x^2} – \cos y
\end{array} \right..$$

با انتگرال‌گیری از معادله اول دستگاه فوق نسبت به متغیر $$x$$، داریم:

$${u\left( {x,y} \right) }={ \int {\left( {2xy – \sin x} \right)dx} }
= {{x^2}y + \cos x + \varphi \left( y \right).}$$

اگر عبارت اخیر را در معادله دوم دستگاه قرار دهیم، به معادله زیر خواهیم رسید:

$${{\frac{{\partial u}}{{\partial y}} }={ \frac{\partial }{{\partial y}}\left[ {{x^2}y + \cos x + \varphi \left( y \right)} \right] }={ {x^2} – \cos y,\;\;}}\\\Rightarrow
{{\cancel{x^2} + \varphi’\left( y \right) }={ \cancel{x^2} – \cos y,\;\;}}\\ \Rightarrow
{\varphi’\left( y \right) = – \cos y.}$$

بنابراین:

$${\varphi \left( y \right) = \int {\left( { – \cos y} \right)dy} }={ – \sin y.}$$

در نتیجه، تابع $$u\left( {x,y} \right)$$ به‌صورت زیر به‌دست می‌آید:

$${{x^2}y + \cos x – \sin y }={ C.}$$

در نهایت، جواب عمومی معادله دیفرانسیل، با فرمول ضمنی زیر بیان می‌شود:

$${{x^2}y + \cos x – \sin y }={ C.}$$

مثال ۵

معادله دیفرانسیل زیر را حل کنید:

$$\left( {1 + 2x\sqrt {{x^2} – {y^2}} } \right)dx -2y\sqrt {{x^2} – {y^2}} dy=0$$

حل: ابتدا باید کامل بودن معادله را بررسی کنیم:

$${\frac{{\partial Q}}{{\partial x}} }={ \frac{\partial }{{\partial x}}\left( { – 2y\sqrt {{x^2} – {y^2}} } \right) }
= { – 2y \cdot \frac{{2x}}{{2\sqrt {{x^2} – {y^2}} }} }
= { – \frac{{2xy}}{{\sqrt {{x^2} – {y^2}} }},}\\
{\frac{{\partial P}}{{\partial y}} }={ \frac{\partial }{{\partial y}}\left( {1 + 2x\sqrt {{x^2} – {y^2}} } \right) }
= {2x \cdot \frac{{\left( { – 2y} \right)}}{{2\sqrt {{x^2} – {y^2}} }} }
= { – \frac{{2xy}}{{\sqrt {{x^2} – {y^2}} }}.}$$

همان‌گونه که می‌بینیم، تساوی $${\large\frac{{\partial Q}}{{\partial x}}\normalsize} = {\large\frac{{\partial P}}{{\partial y}}\normalsize}$$ برقرار و معادله کامل است.

در ادامه، تابع $$u\left( {x,y} \right)$$ را به‌گونه‌ای محاسبه می‌کنیم که در دستگاه زیر صدق کند:

$$\left\{ \begin{array}{l}
\frac{{\partial u}}{{\partial x}} = 1 + 2x\sqrt {{x^2} – {y^2}} \\
\frac{{\partial u}}{{\partial y}} = – 2y\sqrt {{x^2} – {y^2}}
\end{array} \right..$$

با انتگرال‌گیری از معادله اول، داریم:

$${u\left( {x,y} \right) \text{ = }}\kern0pt{ \int {\left( {1 + 2x\sqrt {{x^2} – {y^2}} } \right)dx} } \\
= {x + \frac{{{{\left( {{x^2} – {y^2}} \right)}^{\frac{3}{2}}}}}{{\frac{3}{2}}} + \varphi \left( y \right) } \\
= {x + \frac{2}{3}{\left( {{x^2} – {y^2}} \right)^{\frac{3}{2}}} }+{ \varphi \left( y \right)}$$

که در آن، $$\varphi \left( y \right)$$ یک تابع مجهول از $$y$$ است که باید آن را پیدا کنیم.

اکنون، نتیجه به‌دست‌آمده را در معادله دوم دستگاه جایگذاری می‌کنیم:

$${{\frac{{\partial u}}{{\partial y}} }={ \frac{\partial }{{\partial y}}\Big[ {x + \frac{2}{3}{{\left( {{x^2} – {y^2}} \right)}^{\frac{3}{2}}} }}+{{ \varphi \left( y \right)} \Big] = – 2y\sqrt {{x^2} – {y^2}} ,\;\;}}\\\Rightarrow
{{ – \cancel{2y\sqrt {{x^2} – {y^2}}} + \varphi’\left( y \right) }={ – \cancel{2y\sqrt {{x^2} – {y^2}}} ,\;\;}}\\ \Rightarrow
{\varphi’\left( y \right) = 0.}$$

با انتگرال‌گیری از عبارت اخیر، داریم:

$$\varphi \left( y \right) = C$$

که در آن، $$C$$ یک ثابت است.

در نتیجه، جواب عمومی معادله دیفرانسیل، به‌فرم زیر است:

$${x + \frac{2}{3}{\left( {{x^2} – {y^2}} \right)^{\frac{3}{2}}} }+{ C }={ 0.}$$

مثال ۶

معادله دیفرانسیل زیر را با شرط اولیه $$y\left( 1 \right) = 1$$ حل کنید:

$${\large\frac{1}{{{y^2}}}\normalsize} – {\large\frac{2}{x}\normalsize} ={\large\frac{{2xy’}}{{{y^3}}}\normalsize}$$

حل: ابتدا معادله را به‌فرم استاندارد می‌نویسیم:

$${\frac{1}{{{y^2}}} – \frac{2}{x} = \frac{{2x}}{{{y^3}}}\frac{{dy}}{{dx}},\;\;}\\ \Rightarrow
{\left( {\frac{1}{{{y^2}}} – \frac{2}{x}} \right)dx = \frac{{2x}}{{{y^3}}}dy,\;\;}\\ \Rightarrow
{\left( {\frac{1}{{{y^2}}} – \frac{2}{x}} \right)dx – \frac{{2x}}{{{y^3}}}dy }={ 0.}$$

مشتقات جزئی مربوط به آزمون کامل بوده، به‌صورت زیر هستند:

$${{\frac{{\partial Q}}{{\partial x}} }={ \frac{\partial }{{\partial x}}\left( { – \frac{{2x}}{{{y^3}}}} \right) }={ – \frac{2}{{{y^3}}},\;\;\;}}\kern-0.3pt
{{\frac{{\partial P}}{{\partial y}} }={ \frac{\partial }{{\partial y}}\left( {\frac{1}{{{y^2}}} – \frac{2}{x}} \right) }={ – \frac{2}{{{y^3}}}.}}$$

در نتیجه، معادله کامل است. اکنون دستگاه معادلات زیر را برای یافتن تابع $$u\left( {x,y} \right)$$ تشکیل می‌دهیم:

$$\left\{ \begin{array}{l}
\frac{{\partial u}}{{\partial x}} = \frac{1}{{{y^2}}} – \frac{2}{x}\\
\frac{{\partial u}}{{\partial y}} = – \frac{{2x}}{{{y^3}}}
\end{array} \right..$$

در ادامه، با انتگرال‌گیری از معادله دوم نسبت $$y$$، تابع مورد نظر را محاسبه می‌کنیم:

$${u\left( {x,y} \right) }={ \int {\left( { – \frac{{2x}}{{{y^3}}}} \right)dy} }
= {\frac{x}{{{y^2}}} + \psi \left( x \right).}$$

با مشتق‌گیری از معادله اخیر نسبت به متغیر $$x$$، داریم:

$${{\frac{{\partial u}}{{\partial x}} }={ \frac{\partial }{{\partial x}}\left[ {\frac{x}{{{y^2}}} + \psi \left( x \right)} \right] }={ \frac{1}{{{y^2}}} – \frac{2}{x},\;\;}}\\ \Rightarrow
{{\cancel{\frac{1}{{{y^2}}}} + \psi’\left( x \right) }={ \cancel{\frac{1}{{{y^2}}}} – \frac{2}{x},\;\;}}\\ \Rightarrow
{\psi’\left( x \right) = – \frac{2}{x},\;\;}\Rightarrow
{{\psi \left( x \right) = – 2\ln \left| x \right| }={ \ln \frac{1}{{{x^2}}}.}}$$

در نهایت، جواب عمومی معادله دیفرانسیل، به‌فرم ضمنی زیر به‌دست می‌آید:

$$\frac{x}{{{y^2}}} + \ln \frac{1}{{{x^2}}} = C.$$

جواب خصوصی را نیز می‌توان با استفاده از شرط اولیه $$y\left( 1 \right) = 1$$ محاسبه کرد. با جایگذاری شرط اولیه، مقدار $$C$$ محاسبه می‌شود:

$${\frac{1}{{{1^2}}} + \ln \frac{1}{{{1^2}}} = C,\;\;}\Rightarrow
{1 + 0 = C,\;\;}\Rightarrow
{C = 1.}$$

بنابراین، جواب نهایی با در نظر گرفتن شرایط اولیه، به‌صورت زیر است:

$$\frac{1}{{{y^2}}} + \ln \frac{1}{{{x^2}}} = 1.$$

اگر این مطلب برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس ریاضیات
• مجموعه آموزش‌های ریاضیات و فیزیک پایه
• مجموعه آموزش های معادلات دیفرانسیل به همراه حل نمونه سئوالات آزمون کارشناسی ارشد
• آموزش ریاضی پایه دانشگاهی
• دستگاه معادلات دیفرانسیل خطی — به زبان ساده
• معادله دیفرانسیل بسل — به زبان ساده
• معادلات دیفرانسیل ضمنی — به زبان ساده

^^

سید سراج حمیدی (+)

«سید سراج حمیدی» دانش‌آموخته مهندسی برق است. او مدتی در زمینه انرژی‌های تجدیدپذیر فعالیت کرده، و در حال حاضر، آموزش‌های ریاضیات، مهندسی برق و بورس مجله فرادرس را می‌نویسد.

بر اساس رای 26 نفر

آیا این مطلب برای شما مفید بود؟