تعداد بازدید ها: 11,422
در این مطلب قصد داریم تا یکی از مفاهیم بنیادی حساب دیفرانسیل و انتگرال را توضیح دهیم. مفهوم دیفرانسیل تابع پیشزمینهای برای مشتق و شیب خط بوده و آموزش آن به منظور یادگیری مفاهیم حسابان ضروری است.
محتوای این مطلب جهت یادگیری بهتر و سریعتر آن، در انتهای متن به صورت ویدیویی نیز ارائه شده است.
برای مشاهده ویدیوها کلیک کنید.
تعریف دیفرانسیل تابع
تابعی همچون $$ \large y = f \left ( x \right ) $$ را به صورتی در نظر بگیرید که در بازه $$ \large \left[ {a , b} \right] $$ پیوسته است. فرض کنید در نقطهای همچون $$ \large { x _ 0 } \in \left [ { a , b } \right] $$، جابجایی اندک $$ \large Δ x $$ نشان دهنده فاصله بین دو نقطه $$ \large x _ 0 $$ و نقطه همسایهاش یعنی $$ \large x _ 0 + \Delta x $$ باشد. در این صورت تغییرات اندک $$ \large Δ y $$ را میتوان به صورت زیر و بر حسب $$ \large Δ x $$ بیان کرد:
$$ \large { \Delta y = \Delta f \left( { {x _ 0 } } \right) } = { f \left( { { x _ 0 } + \Delta x} \right) – f\left( { { x _ 0 } } \right ) } $$
به ازای هر تابع مشتقپذیر، افزایش جزئی $$ \large Δ y $$ را میتوان به صورت مجموع دو عبارت زیر بیان کرد:
$$ \large { \Delta y } = { A \Delta x + \omicron \left ( { \Delta x } \right) } $$
رابطه ۱
بدیهی است که ترمِ اول به صورت خطی به $$ \large Δ x $$ وابسته بوده و جمله ترمِ دوم نیز از مرتب $$ \large Δ x $$ است. ترمِ اول یا همان $$ \large A \Delta x $$ تحت عنوان دیفرانسیل تابع شناخته شده و به صورت یکی از حالات زیر نشان داده میشود.
$$ \Large d y \ \ , \ \ d f ( x _ 0 ) $$
به منظور درک مفهوم دیفرانسیل تابع، مربعی به ضلع ۱ متر را در نظر بگیرید. بدیهی است که مساحت این مربع برابر است با:
$$ \large { S _ 0 } = x _ 0 ^ 2 = 1 \, \text{m} ^ 2 $$
بنابراین $$ S $$ تابعی محسوب میشود که وابسته به طول یا همان $$ \large x _ 0 $$ است. حال فرض کنید ابعاد مربع فوق به اندازه $$ \large \Delta x = 1 \, \text{cm} $$ تغییر کند. در این صورت مساحت جدید آن برابر است با:
$$ \large S = { x ^ 2 } = { \left ( { { x _ 0 } + \Delta x } \right ) ^ 2 } = {1,{01^2} }\kern0pt{\text{= } 1,0201 \,\text{m}^2 }\;\; $$
در حقیقت افزایش مساحتِ $$ \large \Delta S $$ برابر است با:
$$ \large { \Delta S = S – { S _ 0 } } = { 1,0201 – 1 } = { 0,0201\,\text{m}^2 }
= {201 \,\text{cm} ^ 2 } $$
بنابراین دیفرانسیل $$ \large \Delta S $$ را میتوان به صورت زیر بیان کرد.
$$ \large \begin {align*} \require{cancel}
{\Delta S = S – { S _ 0 } } = { {\left( {{x_0} + \Delta x} \right)^2} – x_0^2 }
& = {\cancel{x_0^2} + 2{ x _ 0 } \Delta x + {\left( {\Delta x} \right)^2} – \cancel{x_0^2} }
\\ & = {2 { x _ 0 } \Delta x + {\left( {\Delta x} \right ) ^ 2 } }
\\ & = { A \Delta x + \omicron \left ( { \Delta x } \right ) }
\\ & = { d y + o\left( { \Delta x} \right) } \end {align*} $$
با توجه به رابطه فوق اندازه دیفرانسیل $$ dy $$ برابر است با:
$$ \large \begin {align*} { d y = A \Delta x } = { 2 { x _ 0 } \Delta x } = { 2 \cdot 1 \cdot 0,01 }={ 0,02 \,\text{m}^2 }={ 200\,\text{cm}^2 } \end {align*} $$
همچنین باقیمانده از مرتبه $$ \large {\Delta x} ^ 2 $$ بوده و به صورت زیر بدست میآید.
$$ \large { \omicron \left ( { \Delta x } \right ) = { \left ( { \Delta x } \right ) ^ 2 } } = { {0,01 ^ 2 } = 0,0001\,\text{m}^2 }={ 1\,\text{cm}^2 } $$
توجه داشته باشید که در این مثال اندازه $$ A $$ برابر با مشتق $$ S $$ در نقطه $$ \large x _ 0 $$ است. این مشتق برابر است با:
$$ \large A = 2 { x _ 0 } $$
بنابراین برای هر تابع مشتقپذیر گزاره زیر را میتوان بیان کرد:
ضریب $$ A $$ در رابطه مربوط به تغییرات یک تابع در نقطه $$ \large { x _ 0 } $$ برابر با مشتق تابع $$ \large f $$ در نقطه مذکور است. نهایتا تغییرات اندک تابع $$ \large f $$ در نقطه $$ \large { x _ 0 } $$ برابر است با:
$$ \large { \Delta y = A \Delta x + \omicron\left( {\Delta x} \right) }
= {f ^ { \prime } \left( { { x _ 0 } } \right ) \Delta x + \omicron\left( {\Delta x} \right) } $$
با تقسیم کردن طرفین رابطه فوق به مقدار غیر صفر $$ \large \Delta x \ne 0 $$، به عبارت زیر میرسیم.
$$ \large { \frac { { \Delta y } } { { \Delta x } } = A + \frac{{\omicron\left( {\Delta x} \right ) } } {{\Delta x}} }
= {f ^ { \prime } \left ( { { x _ 0 } } \right) + \frac { { \omicron\left( {\Delta x} \right ) } } { { \Delta x } } } $$
در حالتی حدی که $$ \large \Delta x \rightarrow 0 $$ برقرار باشد، مشتق در نقطه $$ \large x _ 0 $$ به صورت زیر بدست میآید.
$$ \large { y ^ { \prime } \left ( { { x _ 0 } } \right) = \lim \limits _ { \Delta x \to 0} \frac{{\Delta y}}{{\Delta x}} }
= { A } = { f ^ { \prime } \left( {{x_0}} \right ) } $$
توجه داشته باشید که در محاسبه حد فوق، عبارتهایی در صورت که از مرتبه $$ { \Delta x } ^ 2 , { \Delta x } ^ 3 , … $$ هستند، برابر با صفر در نظر گرفته شدهاند. اگر این ترمها را با نماد $$ O (\Delta x) $$ نشان دهیم، در حقیقت فرض زیر در نظر گرفته شده است.
$$ \large \lim \limits _ { \Delta x \to 0} \frac { { \omicron \left ( { \Delta x } \right ) } } { { \Delta x } } = 0 $$
زمانی که تغییرات $$ \Delta x $$ به صفر نزدیک میشود، آن را با $$ d x $$ بیان میکنند. بنابراین در این حالت گزاره زیر را میتوان بیان کرد:
$$ \large d x = \Delta x $$
نهایتا مشتق تابع $$ y $$ نیز به صورت زیر بدست میآید.
$$ \large d y = A \Delta x = y ^ { \prime } d x $$
بنابراین همانطور که رابطه فوق نیز بر میآید، مشتق یک تابع برابر با نسبت دو دیفرانسیل است.
مفهوم هندسی دیفرانسیل تابع
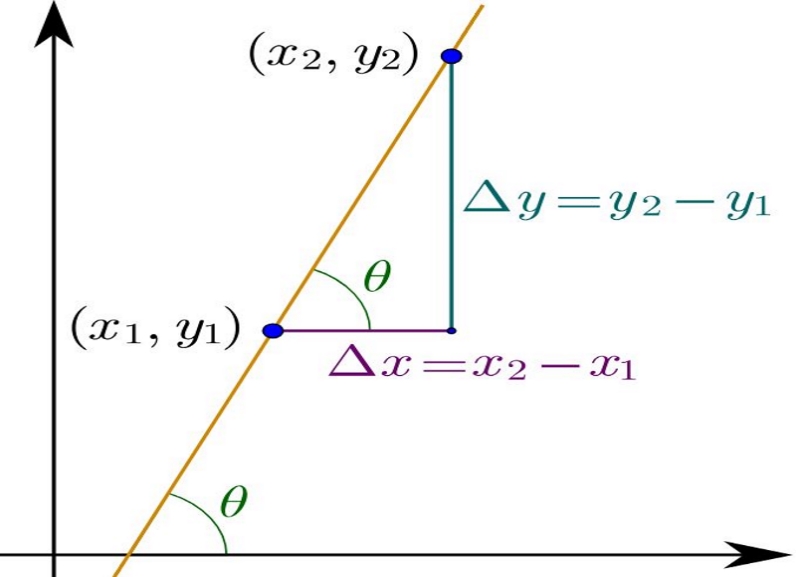
شکل زیر تغییراتِ $$ Δ y $$ را به صورت مجموعِ $$ A Δ x $$ و ترمهای کوچکتر $$ Δx $$ نشان میدهد.
مماسِ $$ MN $$ که بر منحنی $$ \large y= f ( x ) $$، در نقطه $$ M $$ ترسیم شده، دارای شیبی با زاویه $$\large \alpha $$ است. تانژانت این زاویه برابر است با:
$$ \large \tan \alpha = f ^ {\prime} \left ( { { x _ 0 } } \right ) $$
زمانی که متغیر مستقل به اندازه $$Δx$$ تغییر کند، $$y $$ به میزان $$ AΔx $$ تغییر میکند. باقیمانده تغییرات که با خط $$ NM_1 $$ نشان داده شده است، مربوط به ترمهای $$ { \Delta x } ^ 2 , { \Delta x } ^ 3 , … $$ هستند.
ویژگیهای دیفرانسیل تابع
فرض کنید دو تابع $$ u $$ و $$ v $$ وابسته به $$ x $$ باشند. در این صورت دیفرانسیل تابع دارای ویژگیهای زیر است.
- یک ثابت را میتوان از دیفرانسیل خارج کرد. بنابراین رابطه $$ \large d \left( { C u } \right ) = C d u $$ را میتوان برای تابع $$ u $$ بیان کرد.
- دیفرانسیل مجموع دو تابع برابر با مجموع دیفرانسیل دو تابع است. منظور از این گزاره برقرار بودن رابطه $$ \large { d \left ( { u \pm v } \right ) } = { d u \pm d v } $$ است.
- دیفرانسیل یک ثابت برابر با صفر است ($$ \large d ( C ) = 0 $$).
- دیفرانسیل حاصلضرب دو تابع به صورت زیر است.
$$ \large { d \left ( { u v } \right ) } = { d u \cdot v + u \cdot d v } $$ - دیفرانسیل یک تابع کسری همچون $$ \large \frac { u } { v } $$ برابر است با:
$$ \large { d \left ( { \large \frac { u } { v } \normalsize } \right ) } = { \large \frac { { d u \cdot v – u \cdot d v } } { { {v ^ 2 } } } \normalsize.} $$ - دیفرانسیل یک تابع برابر با حاصل ضرب مشتق تابع در دیفرانسیل متغیر مستقل است. بنابراین میتوان گفت:
$$ \large { d y = d f \left( x \right) } = { f ^ { \prime } \left( x \right) d x } $$
دیفرانسیل گیری زنجیرهای
دو تابع ترکیب شده در یکدیگر همچون $$ \large y = f \left ( u \right ) $$ و $$ \large u = g \left ( x \right ) $$ را در نظر بگیرید. در چنین شرایطی مشتق $$ y $$ نسبت به $$ x $$ را میتوان به صورت زیر و با استفاده از مشتقگیری زنجیرهای بر حسب $$ x $$ بدست آورد.
$$ \large { y ^ { \prime } _ x } = { y ^ { \prime } _ u } \cdot {u ^ {\prime} _ x } $$
توجه داشته باشید که در روابط فوق مشتقگیری نسبت به اندیسها انجام شده است. از طرفی دیفرانسیل تابع $$ y $$ را میتوان به صورت زیر نیز بیان کرد:
$$ \large d y = { y ^ { \prime } _ u } \, d u $$
دیفرانسیل $$ u $$ نیز برابر است با:
$$ \large d u = { u ^ { \prime } _ x } \, d x $$
با استفاده از دو رابطه فوق، دیفرانسیل $$ y $$ نسبت به $$ x $$ به صورت زیر قابل محاسبه خواهد بود.
$$ \large { d y = { y ^ { \prime } _ u } \, d u } = { { y ^ { \prime } _ u} { u ^ { \prime } _ x } \, d x } $$
مثال ۱
دیفرانسیل تابع $$ \large y = \sin x – x \cos x $$ را بیابید.
در ابتدا باید مشتق این تابع معلوم شود. بنابراین مشتق y برابر است با:
$$ \large \begin {align*} \require {cancel}
{ y ^ { \prime } = { \left ( { \sin x – x \cos x } \right ) ^ \prime } }
& = {\cos x }-{ \left( {x ^ { \prime } \cos x + x { { \left( {\cos x} \right ) } ^ \prime }} \right) }
\\ & = {\cos x }-{ \left( {\cos x + x\left( { – \sin x} \right)} \right) }
\\ & = {\cancel{\cos x} – \cancel { \cos x } }+{ x \sin x } = { x \sin x } \end {align*} $$
از این رو دیفرانسیل تابع $$ y $$ نیز برابر است با:
$$ \large { d y = y ^ { \prime } d x } = { x \sin x \, d x } $$
مثال ۲
میزان افزایش و دیفرانسیل تابع $$ \large y = {x^2} – x + 1 $$ را در نقطه $$ x=2 $$ به ازای افزایش دیفرانسیلی $$ dx=1 $$ بدست آورید.
همانطور که در بالا بیان شد، افزایش تابع $$ y $$ برابر است با:
$$ \large { \Delta y } = { f \left ( { x + \Delta x } \right ) – f \left ( x \right ) } $$
در این مسئله نقطه همسایگی $$\large x _ 0 $$ در $$ \large { x + \Delta x } = { 2 + 1 = 3 } $$ قرار دارد. بنابراین مقدار تغییرات تابع y برابر است با:
$$ \large { \Delta y = f \left ( 3 \right ) – f \left( 2 \right) }
= { \left ( { { 3 ^ 2 } – 3 + 1} \right) }-{ \left( { { 2 ^ 2 } – 2 + 1} \right) }
= {7 – 3 = 4 } $$
از طرفی به منظور محاسبه دیفرانسیلِ تغییرات تابع در این نقطه باید از مفهوم مشتق استفاده کرد. بنابراین اندازه دیفرانسیل $$ dy $$ در این نقطه برابر است با:
$$ \large \begin {align*} { d y = f ^ {\prime} \left ( x \right ) \Delta x } = { { \left ( { { x ^ 2 } – x + 1 } \right ) ^ \prime } \Delta x }
& = {\left( {2x – 1} \right)\Delta x }
\\ & = {\left( {2 \cdot 2 – 1} \right) \cdot 1 }={ 3 } \end {align*} $$
مثال ۳
دیفرانسیل تابع $$ \large y = x \sin { \large \frac { { \pi x } }{ 2 } \normalsize} $$ را در نقطه $$ \large x = { \large \frac { 1} { 2 } \normalsize } $$ در حالتی بیابید که دیفرانسیل متغیر برابر با $$ \large d x = 0,01 $$ باشد.
دیفرانسیل تغییرات در حالت کلی برابر است با:
$$ \large \begin {align*} {d y = f ^ { \prime } \left ( y \right ) d x } = { { \left ( { x \sin \frac { { \pi x } } { 2 } } \right ) ^ \prime } d x }
& = {\left( {1 \cdot \sin \frac{{\pi x}}{2} }\right.}+{\left.{ x \cdot \cos \frac{{\pi x}}{2} \cdot \frac{\pi }{2}} \right)dx }
\\ & = {\left( {\sin \frac{{\pi x}}{2} }+{ \frac{{\pi x}}{2}\cos \frac{{\pi x}}{2}} \right ) d x } \end {align*} $$
نهایتا با قرار دادن مختصات نقطه در عبارت فوق دیفرانسیل $$ \large d y $$ برابر با مقدار زیر بدست میآید.
$$ \large \begin {align*} { d y } = { \left ( {\sin \frac{{\pi \cdot \frac{1}{2}}}{2} }\right.}+{\left.{ \frac{{\pi \cdot \frac{1}{2}}}{2}\cos \frac{{\pi \cdot \frac{1}{2}}}{2}} \right) \cdot 0,01 }
& = {\left( {\sin \frac{\pi }{4} + \frac{\pi }{4}\cos \frac{\pi }{4}} \right) \cdot}\kern0pt{ 0,01 }
\\ & = {\left( {\frac{{\sqrt 2 }}{2} + \frac{\pi }{4}\frac{{\sqrt 2 }}{2}} \right) \cdot}\kern0pt{ 0,01 }
\\ & = {\frac{{\sqrt 2 }}{{200}}\left( {1 + \frac{\pi }{4}} \right) }\approx{ 0,0126.} \end {align*} $$
در صورت علاقهمندی به مباحث مرتبط در زمینه ریاضی، آموزشهای زیر نیز به شما پیشنهاد میشود:
- مجموعه آموزشهای ریاضی و فیزیک
- مجموعه آموزشهای ریاضی
- مجموعه آموزشهای دروس دبیرستان و پیشدانشگاهی
- دایره مثلثاتی – به زبان ساده
- مشتق توابع معکوس مثلثاتی – به زبان ساده
^^
فیلم های آموزش دیفرانسیل تابع — به زبان ساده (+ دانلود فیلم آموزش رایگان)
فیلم آموزشی تعریف دیفرانسیل تابع
فیلم آموزشی مفهوم هندسی و ویژگیهای دیفرانسیل تابع
فیلم آموزشی دیفرانسیلگیری زنجیرهای
«مجید عوضزاده»، فارغ التحصیل مقطع کارشناسی ارشد رشته مهندسی مکانیک از دانشگاه تهران است. فیزیک، ریاضیات و مهندسی مکانیک از جمله مباحث مورد علاقه او هستند که در رابطه با آنها تولید محتوا میکند.
بر اساس رای 23 نفر
آیا این مطلب برای شما مفید بود؟