روش سیمپسون برای حل انتگرال

در آموزش‌های قبلی مجله فرادرس، درباره انتگرال و روش‌های محاسبه آن بحث کردیم. در این آموزش‌ها، مباحثی مانند انتگرال توابع مثلثاتی، انتگرال‌گیری جزء به جزء، انتگرال دوگانه و انتگرال سه‌گانه را معرفی کردیم. همچنین با تغییر متغیر و کاربرد آن در انتگرال‌گیری آشنا شدیم. گاهی می‌خواهیم ناحیه بین یک منحنی و محور مختصات را محاسبه کنیم، اما نمی‌توانیم حاصل انتگرال مربوط به محاسبه مساحت منحنی را به راحتی و با محاسبه تحلیلی به دست آوریم. یکی از راه‌هایی که در این مواقع وجود دارد، استفاده از روش‌های عددی برای محاسبه انتگرال منحنی است. در این آموزش، یکی از این روش‌ها، یعنی «قاعده سیمپسون» (Simpson’s Rule) را معرفی می‌کنیم.

محتوای این مطلب جهت یادگیری بهتر و سریع‌تر آن، در انتهای متن به صورت ویدیویی نیز ارائه شده است.

برای مشاهده ویدیوها کلیک کنید.

قاعده سیمپسون

در قاعده سیمپسون، از سهمی‌ها برای تقریب هر تکه از منحنی استفاده می‌کنیم. اثبات شده که این روش نسبت به بسیاری از روش‌های مشابه برای محاسبه عددی انتگرال، کارآمدتر و دقیق‌تر است.

فرمول قاعده سیمپسون

مساحت زیر منحنی را به $$n$$ بخش مساوی با عرض $$ \Delta x $$ تقسیم می‌کنیم.

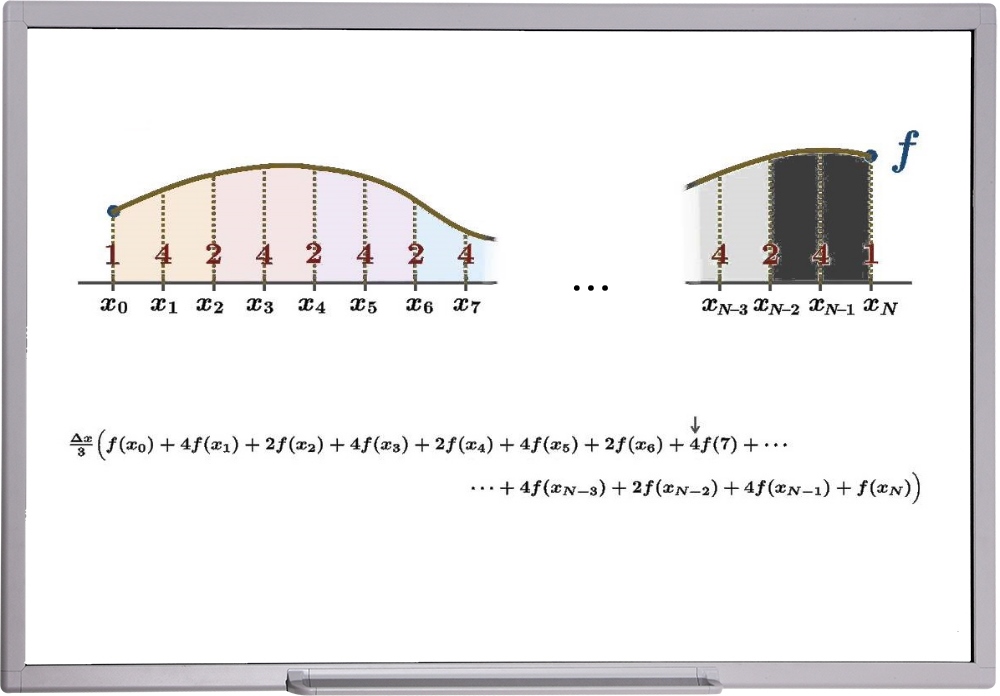
فرمول مساحت تقریبی با استفاده از قاعده سیمپسون به صورت زیر است:

$$ \large \begin {align*}
A \displaystyle = { \int _ { { a } } ^ { { b } } } f { { \left ( { x } \right ) } } { \left . { d } { x } \right . }
\displaystyle \approx \frac { { \Delta { x } }} { {3 } } { \left ( { y } _ { { 0 } } + { 4 } { y } _ { { 1 } } + { 2 } { y } _ { { 2 } } + { 4 } { y } _ { { 3 } } + { 2 } { y } _ { { 4 } } \right . } + \displaystyle { \left . \ldots + { 4 } { y } _ { { { n } – { 1 } } } + { y } _ { { n } } \right ) }
\end {align*} $$

که در آن:

$$ \large \displaystyle \Delta { x } = \frac { { { b } -{ a } } } { { n } } $$

توجه کنید که در قاعده سیمپسون، $$n$$ باید زوج باشد.

برای به خاطر سپردن قاعده سیمپسون، می‌توانیم آن را به صورت زیر بنویسیم:

$$ \large \displaystyle { \int _ { { a } } ^ { { b } } } f { { \left ( { x } \right ) } } { \left . { d } { x } \right . } \displaystyle \approx \frac { { \Delta { x } } } { { 3 } } { \left [ { y } _ { { 0 } } + { 4 } { \left ( { y } _ { { 1 } } + {y } _ {{ 3} } + { y} _ { { 5 } } + \ldots \right ) } \right . }
\displaystyle { \left . + { 2 } { \left ( { y } _ { {2 } } +{ y } _ { { 4 } } + { y } _{ { 6 } } + \ldots \right ) } + { y } _ { { n} } \right ] } $$

یا به عبارت دیگر:

اثبات قاعده سیمپسون

فرض کنید می‌خواهیم مساحت زیر منحنی سهمی $$ \displaystyle { y } = { a } { x } ^ { 2 } + { b } { c }+ { c }$$ را محاسبه کنیم.

برای سادگی، از نقطه $$(0, y_1)$$ شروع کرده و مساحت زیر منحنی را از $$x = – h $$ تا $$ x = h $$ به دست می‌آوریم ($$ \Delta  x = h $$).

بنابراین، داریم:

$$ \large \begin {align*}
\displaystyle { \int _ { { – { h } } } ^ {{ h } } } { \left ( { a } { x } ^ { 2} +{ b } { x } + { c } \right ) } \ { \left . { d} { x }\right . }
\displaystyle & = { { \left [ \frac { { { a } { x } ^ { 3 } } } { { 3 } } + \frac { { { b } { x } ^ { 2 } } } { { 2 } } + { c } { x } \right ] } _ { { – { h } } } ^ { { h } } } \\
\displaystyle & = { \left ( \frac { { { a } { h } ^ { 3} } } { { 3} } + \frac { { { b } { h } ^ { 2 } } } { { 2 } } + { c } { h } \right ) } –
\displaystyle { \left ( – \frac { { { a } { h } ^ { 3 } } } { { 3 } } + \frac {{ { b } { h } ^ { 2 } } } { { 2 } } – { c } { h } \right ) } \\
\displaystyle&=\frac{{{2}{a}{h}^{3}}}{{3}}+{2}{c}{h}
\displaystyle=\frac{h}{{3}}{\left({2}{a}{h}^{2}+{6}{c}\right)} \end {align*} $$

سهمی از سه نقطه $$(-h, y_0)$$، $$(0, y_1) $$ و $$(h, y_2 ) $$ می‌گذرد. با جایگذاری این سه نقطه در معادله عمومی، می‌توان نوشت:

$$ \large \begin {align*}
\displaystyle { y } _ { { 0 } } & = { a } { h } ^ { 2 } – { b } { h } + { c } y \\
\displaystyle { y } _ { { 1 } } & = { c } \\
\displaystyle { y } _ { { 2 } } & = {a } { h } ^ { 2 } + { b } { h } + { c } y
\end {align*} $$

از معادله دوم، داریم:

$$ \large c= y_1 $$

همچنین، مجموع معادله اول و سوم برابر است با:

$$ \large \displaystyle { 2 } { a } { h } ^ { 2 } = { y } _ { { 0 } } – { 2 } { y } _ { { 1 } } + { y} _ { { 2 }} $$

اکنون دو عبارت بالا را در $$ \displaystyle { A } = \frac { h } { { 3 } } { \left ( { 2 }{ a } { h } ^ { 2} + { 6} { c } \right ) } $$ جایگذاری می‌کنیم:

$$ \large \begin {align*}
\displaystyle { A } & = \frac { h } { { 3 } } { \left ( { 2 } { a } { h } ^ { 2 } + { 6 } { c } \right ) } \\
\displaystyle & = \frac { h } { { 3 } } { \left ( { y } _ { { 0 } } – { 2 } { y } _ { { 1 } } + { y } { 2 } + { 6 } { y } _ { { 1 } } \right ) } \\
\displaystyle & = \frac { h } { { 3 } } { \left ( { y } _ { { 0 } } + { 4 } { y } _ { { 1 } } + { y } _ { { 2 } } \right ) }
\end {align*} $$

به طور مشابه، مساحت زیر منحنی سهمی گذرنده از سه نقطه بعدی را محاسبه می‌کنیم:‌

$$ \large \displaystyle { A } = \frac { h } { { 3 } }{ \left ( { y } _ { { 2 } } + { 4 } { y } _ { { 3 } } + { y } _ { { 4 } } \right ) } $$

مجموع دو مساحت برابر است با:

$$ \large \displaystyle { A } = \frac { h } { { 3 } }{ \left ( { y } _ { { 0 } } + { 4 } { y } _ { { 1 } }+ { 2 } { y } _ { { 2 } } + { 4} { y } _ { { 3 } } + { y } _ { { 4 } } \right ) } $$

با در نظر گرفتن شش زیر بازه، سه سهمی خواهیم داشت. مجموع مساحت زیر منحنی این سه سهمی را با طی مراحل قبل می‌توان به صورت زیر به دست آورد:‌

 $$ \large \displaystyle { A } = \frac { h } { { 3 } } { \left [ { y } _ { { 0 } } + { 4 } { y } _ { { 1 } } + { 2 } { y } _ { { 2 } } + { 4 } { y } _ { { 3 } } + \right . }
+ \displaystyle { 2 } { y } _ { {4 } }
+ \displaystyle { 4 } { y } _ { { 5 } }
+ \displaystyle { \left . { y } _ { { 6 } } \right ] } $$

اگر همین مراحل را برای زیر بازه‌های بیشتر تکرار کنیم و مجموع مساحت‌ها را به دست آوریم، می‌توانیم قاعده سیمپسون را به صورت زیر بنویسیم:

$$ \large \displaystyle { \int _ { { a } } ^ { { b } } } f { { \left ( { x } \right ) } } { \left . { d } { x } \right . }
\displaystyle \approx \frac { { \Delta { x } } } { { 3 } } { \left ( { y } _ { { 0 } } + { 4 } { y } _ { { 1 } } + { 2 } {y } _ { { 2 } } + { 4 } { y } _ { { 3 } } + \right . }
+ \displaystyle { 2 } { y } _{ { 4 } } \ldots
+ \displaystyle { 4 } { y }_ { { { n} – { 1 } } }
+ \displaystyle { \left . { y } _{ { n } } \right ) } $$

مثال عددی زیر، نحوه محاسبات در این روش را به خوبی بیان می‌کند.

فرض کنید می‌خواهیم مساحت زیر منحنی عمومی شکل زیر را حساب کنیم.

منحنی بالا را به چهار بخش مساوی تقسیم می‌کنیم (تعداد این بخش‌ها باید عدد زوجی باشد).

در ادامه، سهمی‌هایی را پیدا می‌کنیم که بسیار شبیه به هر یک از چهار تکه منحنی باشند. اگر سه نقطه داشته باشیم، می‌توانیم یک سهمی منحصر به فرد را از آن‌ها عبور دهیم.

از دو تکه اول سمت چپ منحنی شروع می‌کنیم. نقاط میانی و انتهایی را به صورت زیر تعیین می‌کنیم.

فرض می‌کنیم نقاط مورد نظر به صورت زیر باشند:

$$ \large \begin {align*} \displaystyle { \left ( { x } _ { { 0 } } , { y } _ { { 0 } } \right ) } &= { \left ( – { 1.57 } , { 1 } \right ) } \\
\displaystyle { \left ( { x } _ { { 1 } } , { y } _ { { 1 } } \right ) } &= { \left ( – { 0 .3 9 } , { 1.62 } \right ) }
\\
\displaystyle { \left ( { x } _ { { 2 } } , { y } _ { { 2} } \right ) } &= { \left ( { 0.79 } , { 2.71 } \right ) } \end {align*} $$

این سه نقطه را در فرمول یک سهمی به فرم عمومی $$ \displaystyle { y } = { a } { x } ^ { 2 } + { b } { x } + { c } $$ جایگذاری می‌کنیم:

$$ \large \begin {align*} \displaystyle { 1 } & ={ a } { \left ( -{ 1.57 } \right ) } ^ { 2 } + { b } { \left ( – { 1.57 } \right ) }+ { c } \\\displaystyle { 1.62 } & = { a } { \left ( – { 0.39 } \right ) } ^ { 2 } + { b } { \left ( – { 0.39 } \right ) } + { c } \\\displaystyle { 2.71 } & = { a } { \left ( { 0.79 } \right ) }^ { 2 } + { b } { \left ( { 0.79 } \right ) } + { c } \end {align*} $$

معادلات بالا، یک دستگاه سه معادله و سه مجهولی را تشکیل می‌دهند و از آن می‌توان ضرایب $$a$$، $$b$$ و $$c$$ را به دست آورد:

$$ \large \displaystyle { a } = { 0.17021 }, \; \displaystyle { b } = { 0.85820 }, \; \displaystyle { c } = { 1.92808 } . $$

در نتیجه می‌توان معادله سهمی گذرنده از سه نقطه را به صورت زیر نوشت (اعداد گرد شده‌اند):

$$ \large \displaystyle { y } = {0.170 } { x } ^ { 2 } + { 0.858 }{ x } + { 1.93 } $$

منحنی سهمی، در شکل زیر نشان داده شده است:

همان‌طور که می‌بینیم، سهمی از سه نقطه می‌گذرد و بسیار نزدیک به منحنی اصلی است؛ بنابراین، تقریب مناسبی برای این تکه از منحنی است.

فرایند مشابهی را برای دو تکه دیگر انجام می‌دهیم و سهمی گذرنده از سه نقطه را به شکل زیر به دست می‌آوریم:

هرچه تعداد تکه های منحنی بیشتر باشد یا عرض زیر بازه‌ها کمتر باشد، دقت تقریب بالاتر می‌رود. شکل زیر نشان می‌دهد که با کاهش اندازه زیر بازه‌ها، سهمی مشابه منحنی اصلی شده است.

خطا در قاعده سیمپسون

وقتی مقدار عددی انتگرال را تقریب می‌زنیم، همیشه مقداری خطا وجود دارد. این خطا برابر است با:

$$ \large \displaystyle { \large { { E } = { \int _ { { a } } ^ {{ b } } } { f { { \left ( { x } \right ) } } } { d } { x } – { A } { p } { p } } } $$

که در آن، $$ \displaystyle{\large{{A}{p}{p}}} $$ مقدار تقریبی و $$E$$ خطا است.

حال می‌خواهیم بدانیم محدوده خطای قاعده سیمپسون چقدر است. فرض کنید برای $$ \displaystyle { \large { { a } \le { x } \le { b } } } $$ داشته باشیم: $$ \displaystyle { \large { { \left | { { f } } ^ { { { \left ( { 4 } \right) }} } { \left ({ x } \right ) } \right | } \le { M } } } $$. بنابراین، کران خطا به صورت زیر خواهد بود:

$$ \large \displaystyle { \large { { \left | { E } \right | } \le \frac { { { M } { { \left ( { b } – { a } \right ) } } ^ { { 5 } } } } { { { 1 8 0 } { { n } } ^ { { 4 } } } } } } $$

مثال‌ها

در ادامه، مثال‌هایی را از کاربرد قاعده سیمپسون بیان می‌کنیم.

مثال ۱

انتگرال $$ \displaystyle { \int _ { { 2 } } ^ { { 3 } } } \frac { { { \left .{ d } { x } \right . } } } { { { x } + { 1 } } } $$  را با استفاده از قاعده سیمپسون با $$n=4$$ محاسبه کنید.

حل: نمودار منحنی مطابق شکل زیر است:

اندازه هر زیر بازه به صورت زیر تعیین می‌شود:‌

$$ \large \displaystyle \Delta { x } = \frac { { { b } – { a } } } { { n } } = \frac { { { 3 } – { 2 } } } { { 4 } } = { 0 .2 5 }$$

با توجه به عرض هر زیر بازه، نقاط مربوط به هریک از زیر بازه‌ها به صورت زیر است:‌

$$ \begin{align*} \large \displaystyle { y } _ { { 0 } } = f { { \left ( { a } \right ) } }
\displaystyle &= f { { \left ( { 2 } \right ) } }
\displaystyle = \frac { 1 } { { { 2 } + { 1 } } } = { 0.3333333 } \\ \large \displaystyle { y } _ { { 1 } } &= f {{ \left ( { a } + \Delta { x } \right ) } } = f { { \left ( { 2.25 } \right ) } }
\displaystyle = \frac { 1 } { { { 2.25 } + { 1 } } } = { 0.3076923 } \\ \large \displaystyle { y } _ { { 2 } } = f { { \left ( { a } + { 2 } \Delta { x } \right ) } } &= f { { \left ( { 2.5 } \right ) } } ​
\displaystyle = \frac { 1 } { { { 2.5 } + { 1} } } = { 0.2857142 }
\\ \large \displaystyle { y } _ { { 3 } } = f { { \left ( { a } + { 3 } \Delta { x } \right ) } } &= f { { \left ( { 2.75 } \right ) } } \displaystyle = \frac { 1 } { { { 2.75 } + { 1 } } } = { 0.2666667 } \\ \large \displaystyle { y } _ { { 4 } } &= f { { \left ( { b } \right ) } } = f { { \left ( { 3 } \right ) } } \displaystyle = \frac { 1 } { { { 3 } + { 1 } } } = { 0.25 }
\end {align*}$$

بنابراین، طبق قاعده سیمپسون، داریم:

$$ \large \begin {align*} \large A \displaystyle ={ \int _ { { a } } ^ { { b } } } f { { \left ( { x } \right ) } } \text{d}{x}
\displaystyle \approx \frac {0.25 } { { 3 } } { \left ( { 0.333333 } + { 4 } { \left ( { 0.3076923 } \right ) } \right . } \\
\displaystyle + { 2 } { \left ( { 0.2857142 } \right ) } + { 4 }{ \left ( { 0.2666667 } \right ) } \displaystyle { \left . + { 0.25 } \right ) }
\displaystyle = { 0.2876831 }
\end {align*} $$

پاسخ دقیق این مسأله تا شش رقم اعشار، عدد $$ 0.287682 $$ است. بنابراین می‌توان گفت خطای تقریب سیمپسون فقط $$ 0.00036 $$ درصد است.

در این مثال، نمودار بسیار شبیه به یک سهمی است؛ بنابراین، دو سهمی‌ نشان داده شده در شکل، عملاً منحنی $$ \displaystyle { y } = \frac { 1 } { { { x } + { 1 } } } $$ را تشکیل می‌دهند.

مثال ۲

با استفاده از قاعده سیمپسون، مقدار $$ \displaystyle { \large { { \int _ { { 1 } } ^ { { 2 } } } \frac { { 1 } } { { { x } } ^ { { 2 } } } { d } { x } } } $$ را با $$n=8$$ محاسبه کنید.

حل: از آن‌جایی که نقاط ابتدا و انتهای بازه به ترتیب، $$a=1$$ و $$b=2$$ هستند و داریم: $$ \displaystyle { \large { { f { { \left ( { x } \right ) } } } = \frac { { 1 } } { { { x } } ^ { { 2} } } } } $$ و $$n=8$$، می‌توان نوشت:

$$ \large \displaystyle { \large { \Delta { x } = \frac { { { b } – { a } } } { { n } } = \frac { { { 2 } – {1 } } } { { 8 } } = { 0.125 } } } $$

بنابراین، حاصل انتگرال برابر است با:‌

$$ \large \begin {align*}
\int _ { { 1 } } ^{ { 2 } } \frac { { 1 } } { { x } } { \left ( { d } { x } \right ) } \approx { S } _ { { n } }
&= \frac { { { 0.125 } } } { { 3 } } { \left ( { f { { \left ( { 1 } \right ) } } } + { 4 } { f { { \left ( { 1.125 } \right ) } } } + { 2 } { f { { \left ( { 1.25 } \right ) } } } + { 4 } { f { { \left ({ 1.375 } \right ) } } } \\
+ { 2 } { f { { \left ( { 1.5 } \right ) } } } + { 4 } { f { { \left ( { 1.625 } \right ) } } } + { 2 } { f { { \left ( { 1.75 } \right ) } } } + { 4 } { f { { \left ( { 1.875 } \right ) } } } + { f { { \left ( { 2 } \right ) } } } \right ) } \\
&= \frac { { 0.125 } } { { 3 } } { \left ( \frac { { 1 } } { { { 1} } ^ { { 2 } } } + \frac { { 4 } }{ { { \left ( { 1.125 } \right ) } } ^ { { 2 } } } + \frac { { 2 } } { { { \left ( {1.25 } \right ) } } ^ { {2 } } } + \frac { {4 } }{ {{ \left ( {1.375 } \right ) } } ^ {{ 2 } } } + \frac {{ 2 } }{ { { \left ( { 1.5 } \right ) } } ^ { { 2 } } } \\
+ \frac { { 4 } }{ { { \left ( { 1.625 } \right ) } } ^ { {2 } } } + \frac { { 2 }} { {{ \left ( { 1.75 } \right ) } }^ { { 2} }} + \frac { { 4} } {{ { \left ( { 1.875 } \right ) } } ^ {{ 2 }} } + \frac { { 1} } { { { 2 } } ^ { { 2 } } } \right ) } \\ & \approx 0.5000299.
\end {align*} $$

مقدار واقعی انتگرال، $$ \displaystyle { \large { { I } = { \int _ { { 1 } } ^ { { 2 } } } \frac { { 1 } } { { { x } } ^ { { 2 } } } { d } { x } = { 0 . 5 } } } $$ است. همان‌طور که می‌بینیم، قاعده سیمپسون تقریب بسیار مناسبی را ارائه می‌دهد.

مثال ۳

مقدار $$n$$ را به گونه‌ای محاسبه کنید که تقریب قاعده سیمپسون برای انتگرال $$ \displaystyle { \large { { \int _ { { 1 } } ^ { { 2 } } } \frac { { 1 } } {{ { x } } ^ { { 2 } } } { d } { x } } } $$ برابر با مقدار $$0.0002 $$ باشد.

حل: در این مثال، داریم:

$$ \large \displaystyle { \large { { a } ={ 1 } } }, \,\, \displaystyle { \large { { b } = { 2 } } ,\,\,} \displaystyle { \large { { f { { \left ( { x } \right ) } } } = \frac { { 1 } }{ { { x} } ^ { { 2 } } } }} $$

مشتق‌های اول تا چهارم انتگرال‌ده به صورت زیر هستند:‌

$$ \large \displaystyle { \large { { f ^ {\prime} } { \left ( { x } \right ) } = – \frac { { 2 }} { { { x } } ^ { { 3 } } } } } , \,\, \displaystyle { \large {{ f ^ {\prime \prime}} { \left ( { x } \right ) } = \frac { { 6 } } { { { x } } ^ { { 4 } } } } } , \, \, \displaystyle { \large { { f ^ {\prime \prime \prime} } { \left ( { x } \right ) } = – \frac { { 2 4 } } { {{ x } } ^{ { 5 }} }} } , \, \, \displaystyle { \large { { { f} } ^ {{ { \left ( { 4 } \right ) } } }{ \left ( { x } \right ) } = \frac { { 1 2 0 } } { { { x } } ^ { { 6 } } }} } . $$

طبق فرمولی که در بالا معرفی کردیم، داریم:

$$ \large \displaystyle { \large { { \left | { { f } } ^ { { { \left ( { 4 } \right ) } }} { \left ( { x } \right ) } \right | } \le { 1 2 0 } } } , \, \, \displaystyle { \large { { 1 } \le { x } \le { 2 } } } $$

بنابراین، می‌توانیم بنویسیم:

$$ \large \displaystyle { \large { \frac { { { 1 2 0 } { { \left ( { 2 } – { 1 } \right ) } } ^ { { 5 } } } } {{ {1 8 0 } { { n } } ^ { { 4 } } } } < { 0 .0 0 02 } } } $$

یا

$$ \large \displaystyle { \large { { { n } } ^ { { 4 } } > \frac { { 1 20 } } {{ {1 8 0 } \cdot { 0.0 0 0 2 } } } = \frac { { 1 } } { { { 0.0 0 0 3 } } } } } $$

در نتیجه:

$$ \large \displaystyle { \large { { n } > \frac { { 1 } } { { { \sqrt [ { { 4 } } ] { { { 0.0 0 0 3 } }} } } } \approx { 7.6 } } } $$

از آن‌جایی که مقدار $$n$$ باید زوج باشد، $$n=8$$ را انتخاب می‌کنیم.

مثال ۴

با در نظر گرفتن $$n=4$$، مقدار تقریبی انتگرال $$ \int_{{\,0}}^{{\,2}}{{{{\bf{e}}^{{x^2}}}\,dx}}$$ را محاسبه کنید.

حل: ابتدا طول هر زیر بازه را با توجه به $$n=4 $$ محاسبه می‌کنیم:

$$ \large \Delta x = \frac { { 2 – 0 } } { 4 } = \frac { 1 } { 2 } $$

زیر بازه‌ها به صورت زیر هستند:‌

$$ \large \left [ { 0 , \, \, 0.5 } \right ] , \, \, \left [ { 0.5 , \, \, 1 } \right ] , \, \, \left [ { 1 , \, \, 1.5 } \right ] , \, \, \left [ { 1.5 , \, \, 2 } \right] $$

با استفاده از فرمول قاعده سیمپسون، مقدار انتگرال به صورت زیر محاسبه می‌شود:

$$ \large \begin{align*}\int _ { { \, 0 } } ^ { { \, 2 } }{ { { { \bf { e } } ^ { { x ^ 2 } } } \, d x } } &\approx \frac { { { 1 } / { 2 } \; } } { 3 } \left ( { { { \bf { e } } ^ { { { \left ( 0 \right ) } ^ 2 } } } + 4 { { \bf { e } } ^ { { { \left ( { 0.5 } \right ) } ^ 2 } } } + 2 { { \bf { e } } ^ { { { \left ( 1 \right ) } ^ 2 } } } + 4 { { \bf { e } } ^ { { { \left ( {1.5} \right ) } ^ 2 } } } + { { \bf { e } } ^ { { { \left ( 2 \right ) } ^ 2 } } } } \right ) \\ &= 17.35362645 \end{align*} $$

مقدار واقعی انتگرال برابر است با:

$$ \large \int _ { { \, 0 } } ^ { { \, 2 } }{ { { { \bf { e } }^ { { x ^ 2 } } } \, d x } } = 16.45262776 $$

بنابراین، مقدار خطای قاعده سیمپسون $$0.90099869 $$ است.

پیاده‌سازی نر‌م‌افزاری قاعده سیمپسون

در این بخش، شیوه پیاده‌سازی قاعده سیمپسون را در پایتون و متلب بیان می‌کنیم.

پیاده‌سازی در پایتون

ابتدا کتابخانه‌های لازم را فراخوانی می‌کنیم:

برای نوشتن برنامه قاعده سیمپسون در پایتون، ابتدا تابع simps را تعریف می‌کنیم که پارامترهای ورودی آن $$f$$، $$a$$، $$b$$ و $$N$$ هستند و تقریب $$S_N(f) $$ را به عنوان خروجی به دست می‌دهد. مقدار $$N=50$$ را در نظر می‌گیریم. برنامه به صورت زیر است:

اکنون برنامه بالا را برای انتگرالی که مقدار آن را می‌دانیم، آزمایش می‌کنیم. برای مثال، انتگرال زیر را در نظر بگیرید:

 $$ \large \int_0^1 3x^2 dx = 1 $$

برنامه و نتیجه اجرای آن برای این انتگرال به صورت زیر است:

برای انتگرال زیر نیز برنامه را اجرا می‌کنیم:‌

$$ \large \int_0^{\pi/2} \sin(x) dx = 1 $$

در نتیجه، داریم:

پیاده‌سازی در متلب

برنامه متلب قاعده سیمپسون نیز به صورت زیر است:

در آموزش‌های بعدی، روش‌های دیگر محاسبه عددی انتگرال را معرفی خواهیم کرد.

اگر این مطلب برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس ریاضیات
• آموزش محاسبات عددی با MATLAB
• مجموعه آموزش‌های محاسبات عددی
• آموزش ریاضی پایه دانشگاهی
• روش نیوتن — به زبان ساده
• معادله خط — به زبان ساده
• دستگاه معادلات خطی — به زبان ساده
• جذر یا محاسبه ریشه دوم عدد — به زبان ساده

^^

فیلم‌ های آموزش قاعده سیمپسون — به زبان ساده (+ دانلود فیلم آموزش گام به گام)

فیلم آموزشی فرمول قاعده سیمپسون و اثبات آن

فیلم آموزشی حل مثال از الگوریتم سیمپسون

فیلم آموزشی خطا در قاعده سیمپسون

فیلم آموزشی کدنویسی الگوریتم سیمپسون در نرم افزار متلب

سید سراج حمیدی (+)

سید سراج حمیدی دانش‌آموخته مهندسی برق است و به ریاضیات و زبان و ادبیات فارسی علاقه دارد. او آموزش‌های مهندسی برق، ریاضیات و ادبیات مجله فرادرس را می‌نویسد.

بر اساس رای 10 نفر

آیا این مطلب برای شما مفید بود؟