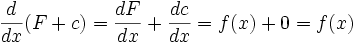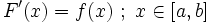خواص انتگرال

اگر 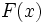پاد مشتق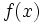باشد ، آنگاه 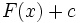به ازای هر مقدار ثابت 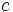یک پاد مشتق 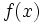است.زیرا اگر 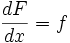آنگاه:

نکته

اگر 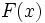جوابی برای باشد ، فرمول 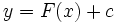همه جوابها را به دست می‌دهد.

مجموعه همه پاد مشتق‌های یک تابع چون 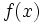را انتگرال نامعین 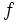نسبت به 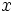می‌نامند و با 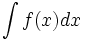نشان می‌دهند.
هرگاه فرمول 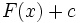همه پادمشتق‌های 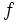را به دست دهد، آنرا چنین مشخص می‌کنیم :

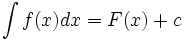
تابع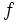 را انتگرال ده انتگرال و 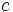را ثابت انتگرال‌گیری می‌نامیم. همچنین 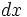نشان می‌دهد که متغیر انتگرال‌گیری 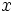است.

1. یک ثابت را می‌توان از زیر نماد انتگرال‌گیری بیرون آورد.(توجه شود که عباراتی را که توابعی از متغیر انتگرال‌گیری اند ، نمی‌توان از زیر نماد انتگرال‌گیری بیرون آورد.)

2. انتگرال مجموع دو تابع برابر مجموع انتگرال‌های آنهاست.این مطلب را میتوان به مجموع هر تعداد متناهی از توابع تعمیم داد.

فرمول های انتگرال گیری

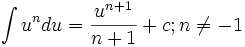
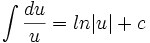
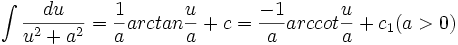
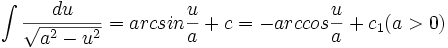
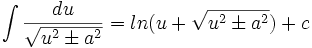
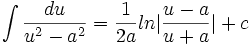
در این دستور‌ها 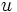یا متغیر مستقل است و یا تابعی مشتق‌پذیر از متغیر مستقل دیگری است.
اگر 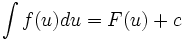آنگاه

در حل یک معادله دیفرانسیل مانند 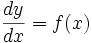معمولا به دنبال جواب خاصی هستیم که شرایط عددی از پیش تعیین شده را برآورده سازد.بدین منظور نخست جواب عمومی 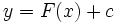را تعیین می‌کنیم که همه جوابهای ممکن را به دست می‌دهد . سپس مقداری از 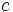را تعیین می‌کنیم که جواب خاص مطلوب را به دست دهد.
اگر نقطه‌ای چون 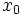از دامنه 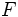را در نظر بگیریم و مقدار دلخواه 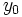را برگزینیم ، می‌توان با قرار دادن 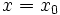و 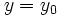در معادله 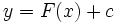و حل آن نسبت به 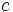جوابی را یافت که از نقطه 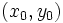بگذرد.به این ترتیب داریم 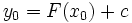یا .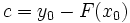
خم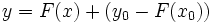 خمی است که از 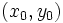می‌گذرد.

در حل انتگرال‌ها با روش تغییر متغیر ، به جای 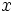تابع پیوسته و مشتق پذیر 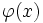را قرار می دهیم، یعنی :

بعد از حل ، بر اساس تابع معکوس ، به جای 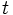نسبت به 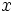قرار می‌دهیم . یعنی: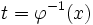
از فرمول فوق به صورت زیر هم می‌توان استفاده کرد:

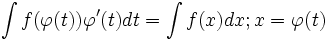
دستور 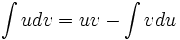موسوم به انتگرال‌گیری به روش جزء به جزء است که در آن 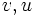توابعی مشتق‌پذیر از 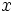هستند. اگر انتگرال به صورت حاصلضرب یک تابع لگاریتمی یا یک تابع معکوس مثلثاتی ، در یک چند جمله ای باشد، در این صورت معمولا 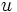را تابع لگاریتمی یا تابع معکوس مثلثاتی انتخاب می‌کنند ولی اگر انتگرال حاصلضرب یک تابع لگاریتمی یا یک تابع نمایی در یک تابع جبری باشد ، معمولا تابع جبری را 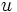فرض می‌کنند.

برای آنکه بتوانیم مساحت شکل مسطح را حساب کنیم واحدی برای مساحت در نظر می‌گیریم که عبارت است از مساحت مربعی که طول اضلاع آن مساوی واحد می‌باشد. اگر مثلا اینچ را واحد طول گرفته باشیم واحد مساحت نظیر آن عبارت است از اینچ مربع یعنی مساحت مربعی که طول اضلاع آن یک اینچ می‌باشد. بر مبنای این تعریف به آسانی می‌توان مساحت هر مربع مستطیل را حساب کرد.

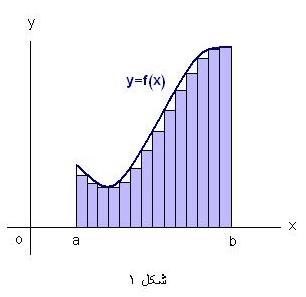
اولین مفهوم اساسی حساب دیفرانسیل و انتگرال عبارت از مفهوم انتگرال می‌باشد. در این مبحث انتگرال را به عنوان اندازه مساحت سطحی که در زیر منحنی مفروض قرار گرفته است و به صورت حدی در نظر خواهیم گرفت اگر یک تابع مثبت و اتصالی y=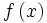 داده شده باشد در این صورت مساحتی را در نظر می‌گیریم که در زیر این منحنی واقع است و از طرف پایین ، قطعه خطی واقع بر محور x ها محدود می‌شود که ما بین دو نقطه به طولهای a ، b و b>a واقع است و از طرفین به دو خط عمود بر محور xها که از این دو نقطه رسم شوند محدود است. هدف ما آن است که مساحت این سطح را که A نامیده می‌شود حساب کنیم.

نخست به تعریف مساحت ناحیه محصور بین نمودار یک تابع پیوسته نامنفی مانند 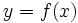و بازه ای از محور مانند 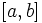می پردازیم.
برای این منظور تا آنجا که می توانیم (طبق شکل 1) بخش هرچه بیشتری از این ناحیه را با مستطیل های محاطی قائم پر می کنیم. مجموع مساحت های مستطیل ها تقریبی است از مساحت ناحیه.هرچه تعداد مستطیل ها بیشتر باشد، تقریب بهتری به دست می آید. بنا به تعریف، مساحت این ناحیه، حد مجموع مساحت های مستطیل هاست وقتی که مستطیل ها کوچک و کوچک تر شوند و تعداد آنها به سوی بی نهایت میل کند.

حال اگر به جای مستطیل های محاطی، مستطیل های محیطی (مطابق شکل 2) و یا هر نوع دیگری از مستطیل ها که قاعده پایین آن ها بر محور ها منطبق و قاعده بالای آن ها خم را قطع کنند به کار ببریم، دقیقا" همان حد به دست می آید.
این نکته نیز شایان ذکر است که حد مجموع مساحت های این مستطیل ها نه تنها برای توابع پیوسته نا منفی – که بحثمان را با آن ها آغاز کردیم – بلکه برای هر تابع پیوسته ای وجود دارد.

مجموع انتگرال بالا – مجموع انتگرال پایین

تابع را در نظر می گیریم که در فاصله 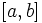تعریف شده است. عبارت

را مجموع انتگرال این تابع گویند که در آن :

مجموع را مجموع (انتگرال) بالا و را مجموع (انتگرال) پایین نامند که در آن :

تابع انتگرال پذیر

حد مجموع انتگرال وقتی را انتگرال معین تابع در فاصله 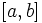گویند.
اگر این حد موجود باشد، تابع را در فاصله 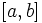انتگرال پذیر گویند.
(نکته : هر تابع پیوسته انتگرال پذیر است.)

دستور زیر معروف به دستور نیوتن-لایپنیتز است :

که در آن 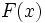یک تابع اولیه تابع می باشد یعنی :

مزایای فرمول نیوتن- لایبنیتز

فرمول نیوتن- لابینیتز هنگامیکه یک تابع اولی تابع انتگرال (تابع زیر علامت انتگرال) معلوم باشد یک روش مناسب و عملی برای محاسبه انتگرالهای معین به دست می‌دهند. در حقیقت انتگرال معین فقط زمانی اهمیت کنونی خود را در ریاضیات کسب کرد که این فرمول توسط نیوتن- لایبنیتز کشف شد. اگر چه پیشینیان (ارشمیدس) از یک عمل مشابه‌ای برای محاسبه انتگرال معین به عنوان حد مجموع انتگرال آگاه بودند، کاربردهای این روش منحصر بود به حالتهای بسیار ساده‌ای که حد مجموع انتگرال می‌توانست مستقیما محاسبه شود. فرمول نیوتن- لایبنیتز دامنه کاربردهای انتگرال معین را تا حد زیاد گسترش داد، زیرا ریاضیات یک روش عمومی برای حل مسائل گوناگون خاصی بدست آورد، و بنابراین توانست بطور قابل ملاحظه‌ای حدود کاربردهای انتگرال معین را در صنعت ، مکانیک ، نجوم و غیره توسعه دهد.

تخمین یک انتگرال معین

1. اگر در فاصله داشته باشیم آنگاه :

و بویژه :

2. اگر 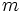کوچکترین و 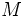بزرگترین مقدار تابع در فاصله 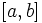باشد، آنگاه :

3.قضیه مقدار میانگین : اگر تابع در فاصله 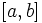پیوسته باشد، آنگاه :

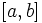4. تعمیم قضیه مقدار میانگین : اگر توابع و در فاصله پیوسته باشند و همچنین علامت در این فاصله ثابت بماند، آنگاه :

5.به ازای هر از نقاط پیوستگی تابع داریم :

تغییر متغیر در انتگرال معین

اگر تابع در شرایط زیر صدق کند :
الف. در فاصله ، تابعی پیوسته و یک مقداری بوده و در این فاصله نیز پیوسته باشد.
ب. اگر 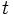در فاصله تغییر نماید، مقادیر تابع از فاصله 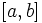خارج نشود.
ج. و
آنگاه دستور تغییر متغییر در انتگرال معین برای هر تابع پیوسته در فاصله 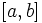بصورت زیر اعمال می شود :

انتگرال در تمام فاصله تفاضل مساحت بالا و پایین محور ox را به دست می دهد. برای پیداکردن مجموع مساحت های سطوح به معنی معمولی، باید مجموع قدر مطلق های انتگرال فواصل جزئی فوق الذکر را به دست آوریم.

فرض می کنیم معادله یک خم در مختصات قطبی است، که در آن یک تابع پیوسته است هنگامیکه α≤θ≤β می باسد. برای به دست آوردن مساخت قطاع محدود شده به وسیله خم و شعاعهای حامل θ=α و θ=β به صورت زیر عمل می کنیم:

طول کمان یک خم در مختصات قائم (کارتزین)

فرض می کنیم معادله یک خم در مختصات قائم باشد. برای محاسبه طول کمان این گونه عمل می کنیم:

با به کاربردن این فرمول اخیر اغلب می توان

مشتق کمان را نسبت به طول به دست آورد.

طول کمان یک خم در مختصات قطبی

فرض می کنیم معادله یک خم در مختصات قطبی باشد، که در آن ρ شعاع حامل و θ زاویه قطبی است. رابطه های بین مختصات قائم ومختصات قطبی چنین اند.

X=f(θ)cosθ , Y=f(θ)sinθ

این معادلات را می توان معادلات پارامتری خم اختیار کرد و با به کاربردن فرمول زیر می توان طول کمان خم را به دست آورد:

• فرض کنید f روی بازه از a تا b پیوسته و نامنفی باشد، اگر ناحیه زیر منحنی در این بازه بسته حول محور x دوران کند، حجم جسم دوار برابر است با:

اگر تابع f حول محور y دوران کند حجم جسم دوار برابر است با: انتگرال نسبت به محور y.

رویه دوار حاصل از دوران خم 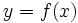حول محور x ها را در نظر می گیریم. مساحت این رویه را به صورت زیر محاسبه می کنیم:

اگر نیروی ثابت F (کیلوگرم) در تغییر مکانی برابر S (متر) عمل کند، کار انجام شده (بر حسب کیلوگرم متر) برابر است با حاصلضرب نیرو در تغییر مکان، یعنی

W=F.S

اما وقتی نیرو ثابت نباشد، مثلا در مواقعی که یک فنررا می کشیم یا فشار می دهیم، نمی توانیم کار انجام شده را مستقیما از رابطه فوق به دست آوریم. ولی اگر نیرو تابع پیوسته ای از S باشد، از رابطه مذکور می توان برای یافتن مقدار تقریبی کار انجام شده در یک تغییر مکان کوتاه، مثلا ∆S استفاده کرد و می توان به روش انتگرال گیری دستور اخیر را برای یافتن مقدار کل کار انجام شده تعمیم داد.

فرض می کنیم جسمی روی خط مستقیمی تحت اثر نیروی متغیر و پیوسته 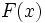حرکت می کند و از نقطه x=a به نقطه x=b می رود. می خواهیم مقدار کار انجام شده توسط نیروی را در این تغییر مکان حساب کنیم.

کار لازم برای تخلیه یک مخزن

کار لازم برای تخلیه کردن مایعی به حجم V و وزن مخصوص w از درون یک مخزن و رساندن آن به ارتفاع h از سطح اولیه مایع از رابطه زیر به دست می آید:

قانون هوک

اگر فنری به طول x بیش از طول طبیعی خود کشیده شود، با نیرویی مساوی kx، به عقب کشیده می شود، که در آن k ثابتی است که به جنس و طول فنر بستگی دارد. قانون هوک، زمانی که فنر به اندازه x فشرده شود نیز برقرار است.

• قضیه: اگر F برآیند همه نیروهای وارد بر متحرکی به جرم m باشد و امتداد F ثابت بماند، آنگاه، مقدار کار انجام شده توسط نیروی F بر آن متحرک، اعم از اینکه نیروی F ثابت باشد یا متغیر، برابر با تغییر انرژی جنبشی آن متحرک است. برای اثبات این قضیه وسایل لازم عبارتند از رابطه کار، تعریف انرژی جنبشی، قانون دوم نیوتن در رابطه

V=ds/dt

یعنی، مقدار کار انجام شده توسط F برابر با انرژی جنبشی در b منهای انرژی جنبشی در a است.

فرض می کنیم دو تابع f و g در بازه a , b پیوسته باشند و برای هر x در این بازه داشته باشیم f(x) ≥ g(x)، برای محاسبه مساحت محصور بین دو منحنی به این صورت عمل می کنیم:

متحرکی با سرعت V=f(t) در فاصله a , b علاوه بر پیوسته بودن مثبت نیز باشد. یعنی جسم تنها در یک جهت حرکت کند و هرگز به عقب برنگردد. اگر S موضع متحرک در لحظه t باشد، پس مسافت پیموده شده توسط متحرک به این صورت به دست می آید:

(S|ab=F(b)-F(a

هرگاه سرعت در بازه باز (a , b) تغییر علامت بدهد، انتگرال فقط مقدار حاصلجمع جبری تغییر S را به دست خواهد داد. در این حالت فواصلی را که به جلو و عقب پیموده می شوند می توان حذف کرد. اگر بخواهیم مقدار واقعی کل مسافت پیموده شده را بیابیم باید انتگرال قدرمطلق سرعت را پیدا کنیم. برای محاسبه این انتگرال باید آن را در روی قسمتهایی که V مثبت و یا منفی است. به طور جداگانه حساب و سپس قدرمطلق نتیجه های حاصل را با هم جمع کنیم.

از مفهوم مقدار میانگین در نظریه های اقتصادی برای بررسی میانگین موجودی روزانه استفاده می شود. اگر تعداد رادیوها یا کفشها یا هر کالای دیگری باشد که کارخانه ای در روز x در اختیار دارد، آنگاه

را میانگین موجودی روزانه آن کالا در مدت a≤x≤b می نامند. هزینه های محل انبارکردن، آب و برق و گاز و تلفن، بیمه، و نگه داری، بخش عمده ای از هزینه های انبارداری است، و موجودی روزانه کارخانه می تواند نقش مهمی در تعیین این هزینه ها داشته باشد. همچنین از مفهوم مقدار میانگین در محاسبه

ولتاژ و جریان موثر در مدارهای الکتریکی استفاده می کنیم.

در تحلیل سازه‌ها و سیستمهای مکانیکی در مهندسی و فیزیک، غالبا جرم آنها را چنان در نظر می گیرند که گویی در یک نقطه متمرکزند. این نقطه را مرکز جرم می نامندو رفتار سیاره ای که دور خورشید می گردد، رفتار یک جرم نقطه ای است که حول جرم نقطه ای دیگر می گردد. وقتی که صفحه ای تخت را روی نوک انگشتان به حالت تعادل در می آوریم، نوک انگشت در مرکز جرم صفحه قرار می گیرد. از انتگرال می توان برای محاسبه گشتاورها و مرکز جرم استفاده کرد. اگر My، Mx و m به ترتیب گشتاور جرم ورقه D نسبت به محور y، گشتاور جرم این ورقه نسبت به محور x و جرم کل ورقه باشد، آنگاه

تاریخچه انتگرال:

بيش از دو هزار سال پيش ارشميدس (287-212 قبل از ميلاد) فرمول هايي را براي محاسبه سطح  وجه ها ، ناحيه ها و حجم هاي جامد  مثل كره ، مخروط و سهمي يافت . روش انتگرال گيري ارشميدس استثنايي و فوق العاده بود جبر ، نقش هاي بنيادي ، كليات و حتي واحد اعشار را هم نمي دانست .

ليبنيز (1716-1646) و نيوتن (1727-1642) حسابان را كشف كردند . عقيده كليدي آنها اين بود كه مشتق گيري و انتگرال گيري اثر يكديگر را خنثي مي كنند با استفاده از اين ارتباط ها آنها توانستند تعدادي از مسائل مهم در رياضي ، فيزيك و نجوم را حل كنند.

فورير (1830-1768) در مورد رسانش گرما بوسيله سلسله زمان هاي مثلثاتي را مي خواند تا نقش هاي بنيادي را نشان دهد .رشته هاي فورير و جابجايي انتگرال امروزه در زمينه هاي مختلفي چون داروسازي و موزيك اجرا مي شود .

گائوس (1855-1777) اولين جدول انتگرال را نوشت و همراه ديگران سعي در عملي كردن انتگرال در رياضي و علوم فيزيك كرد . كايوچي (1857-1789) انتگرال را در يك دامنه همبستگي تعريف كرد . ريمان (1866-1826) و ليبيزگو (1941-1875) انتگرال معين را بر اساس يافته هاي مستدل و منطقي استوار كردند .

ليوويل (1882-1809) يك اسكلت محكم براي انتگرال گيري بوجود آورد بوسيله فهميدن اينكه چه زماني انتگرال نامعين از نقش هاي اساسي دوباره در مرحله جديد خود نقش اساسي مرحله بعد هستند . هرميت (1901-1822) يك شيوه علمي براي انتگرال گيري به صورت عقلي و فكري ( يك روش علمي براي انتگرال گيري سريع ) در دهه 1940 بعد از ميلاد استراسكي اين روش را همراه لگاريتم توسعه بخشيد .

در دهه بيستم ميلادي قبل از بوجود آمدن كامپيوترها رياضيدانان تئوري انتگرال گيري و عملي كردن آن روي جداول انتگرال را توسعه داده بودند و پيشرفت هايي حاصل شده بود .در ميان اين رياضيدانان كساني چون واتسون ، تيچمارش ، بارنر ، ملين ، ميچر ، گرانبر ، هوفريتر ، اردلي ، لوئين ، ليوك ، مگنوس ، آپل بلت ، ابرتينگر ، گرادشتاين ، اكستون ، سريواستاوا ، پرودنيكف ، برايچيكف و ماريچيف حضور داشتند .

در سال 1969 رايسيچ پيشرفت بزرگي در زمينه روش علمي گرفتن انتگرال نامعين حاصل كرد . او كارش را بر پايه تئوري عمومي و تجربي انتگرال گيري با قوانين بنيادي منتشر كرد روش او عملاً در همه گروه هاي قضيه بنيادي كارگر نيست تا زماني كه در وجود آن يك معادله سخت مشتق گيري هست كه نياز دارد تا حل شود . تمام تلاش ها ااز آن پس بر روي حل اين معادله با روش علمي براي موفقيت هاي مختلف قضيه اساسي گذاشته شد . ايت تلاش ها باعث پيشرفت كامل سير و روش علمي رايسيچ شد . در دهه 1980 پيشرفت هايي نيز براي توسعه روش او در موارد خاص از قضيه هاي مخصوص و اصلي او شد .

از قابليت تعريف انتگرال معين به نتايجي دست ميابيم كه نشان دهنده قدرتي است كه در رياضيات مي باشد (1988) جامعيت و بزرگي به ما ديدگاه موثر و قوي در مورد گسترش در  رياضيات و همچنين كارهاي انجام شده در قوانين انتگرال مي دهد . گذشته از اين رياضيات توانايي دارد تا به تعداد زيادي از نتيجه هاي مجموعه هاي مشهور انتگرال پاسخ دهد ( اينكه بفهميم اين اشتباهات ناشي از غلط هاي چاپي بوده است يا نه ) . رياضيات اين را ممكن مي سازد تا هزاران مسئله انتگرال را حل نماييم به طوريكه تا كنون در هيچ يك از كتابهاي دستنويس قبلي نيامده باشد . در آينده ديگر وظيفه ضروري انتگرال اين است كه به ازمايش تقارب خطوط ، ارزش اصلي آن و مكانيسم فرض ها بپردازد

به نقل از وبلاگ اصغری (بلاگفا)